Voici un
d'un polygone à côtés : c'est un
| = |  | 1 2 3 | 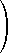 |  | 1 2 3 | 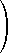 |  | 1 2 3 | 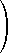 |
= .
Marquer les éléments du sous-groupe engendré par .pour
et appartenant au sous-groupe d'ordre de .Veuillez noter que les pages WIMS sont générées interactivement; elles ne sont pas des fichiers HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE. Il est inutile pour vous de les ramasser par un programme robot.