Intégration numérique

I Introduction

I-2 Notations et définitions

I Introduction

I-3 Résultats fondamentaux

Soit bornée et soit

une subdivision de de pas

On pose:

Définition [Intégrale de Riemann]

La fonction f est dite Riemann intégrable si . Dans ce cas, on note le réel et on l'appelle l'intégrale de Riemann associée à f.

Remarque

Toute fonction continue par morceaux est Riemann intégrable.
Toute fonction monotone est Riemann intégrable.

Intégration numérique

I Introduction

I-2 Notations et définitions

I-1 Problème étudié

I-2 Notations et définitions

I Introduction

I-3 Résultats fondamentaux

I Introduction

I-2 Notations et définitions

Proposition

Si est Riemann intégrable, alors

ou d'une manière équivalente

Remarque

Si est continue alors

Théorème

Si est continue alors

et d'une façon plus générale

Intégration numérique

I Introduction

I-3 Résultats fondamentaux

I-1 Problème étudié

I-3 Résultats fondamentaux

II Formules de quadrature et leur ordre

II Formules de quadrature et leur ordre

II-1 Idée de base

II-1 Idée de base

I Introduction

La plupart des algorithmes numériques procèdent comme suit : on subdivise l'intervalle en plusieurs sous-intervalles et on utilise le fait que

De cette manière, on est amené au calcul de plusieurs intégrales pour lesquelles la longueur de l'intervalle d'intégration est relativement petite. Prenons une de ces intégrales, notons la longueur de l'intervalle et g(t) = f(x_i + t h_i). Un changement de variable nous donne alors:

Il reste alors à calculer une approximation de

Intégration numérique

II-1 Idée de base

II-2 Méthode des rectangles à gauche

II-2 Méthode des rectangles à gauche

I Introduction

L'aire du domaine limité par les droites , l'axe Ox et est approchée par l'aire du rectangle de base

Méthode du rectangle

II-2 Méthode des rectangles à gauche

II-1 Idée de base

II-3 Méthode des rectangles à droite

II-3 Méthode des rectangles à droite

I Introduction

L'aire du domaine limité par les droites , l'axe Ox et est approchée par l'aire du rectangle de base

Intégration numérique

II-3 Méthode des rectangles à droite

II-1 Idée de base

II-4 Méthode du point milieu

II-4 Méthode du point milieu

I Introduction

L'aire du domaine limité par les droites , l'axe Ox et est approchée par l'aire du rectangle de base

Méthode du point milieu

II-4 Méthode du point milieu

II-1 Idée de base

II-5 Méthode du trapèze

II-5 Méthode du trapèze

I Introduction

L'aire du domaine limité par les droites , l'axe Ox et est approchée par l'aire du trapèze de base

Intégration numérique

II-5 Méthode du trapèze

II-1 Idée de base

II-6 Méthode de Simpson

II-6 Méthode de Simpson

I Introduction

Traçons la parabole passant par les trois points . En approchant l'intégrale par l'aire sous la parabole, on obtient la formule de Simpson :

L'aire du domaine limité par les droites , l'axe Ox et est approchée par l'aire grisée.

Intégration numérique

II-6 Méthode de Simpson

II-1 Idée de base

II-7 Méthode de Newton-Cotes

II-7 Méthode de Newton-Cotes

I Introduction

On peut généraliser la méthode de Simpson en approchant l'intégrale par l'aire sous un polynôme de degré s-1 passant par les s points équidistants

on obtient des formules de quadrature appelées formules de Newton-Cotes données par la définition.

Définition

Une formule de quadrature est dite de Newton-Cotes à s étages si elle est de la forme:

Les c_i sont les noeuds de la formule de quadrature et les b_i sont les poids .

Intégration numérique

II-7 Méthode de Newton-Cotes

II-1 Idée de base

II-8 Ordre

I Introduction

Intégration numérique

II-8 Ordre

II-1 Idée de base

II-8 Ordre

II-8-1 Définition

II-8 Ordre

II-8-1 Définition

I Introduction

Définition

On dit que l'ordre ordre d'une formule de quadrature de la formule de quadrature est p si elle est exacte pour tous les polynômes de degré inférieur ou égal à p - 1, c'est-à-dire: pour g polynôme de degré ,

On voit que les formules du point milieu et des trapèzes sont d'ordre 2. La formule de Newton-Cotes à s étages a un ordre p supérieur ou égal à s.

Le tableau suivant résume l'ordre ainsi que les poids des différentes méthodes de quadrature pour

Tableau

s	ordre	b₁	b₂	b₃	b₄	b₅	b₆	b₇	nom
1	1	1							rectangle
1	2	1							pt. milieu
2	2								trapèze
3	4								Simpson
4	4								Newton
5	6								Boole
6	6								Boole
7	8								Weddle

Ordre d'une méthode de quadrature

II-8 Ordre

II-8-1 Définition

II-8-2 Condition nécessaire et suffisante

II-8 Ordre

II-8-2 Condition nécessaire et suffisante

I Introduction

Théorème

La formule de quadrature est d'ordre p si et seulement si:

La nécessité de l'équivalence ) est une conséquence de la formule ) si l'on pose . Pour en montrer la suffisance, on utilise le fait qu'un polynôme de degré p-1 est une combinaison linéaire de et que l'intégrale ainsi que l'expression sont linéaires en g.

Intégration numérique

II-8 Ordre

II-8-2 Condition nécessaire et suffisante

II-8-1 Définition

II-8-3 Remarque sur l'ordre

II-8 Ordre

II-8-3 Remarque sur l'ordre

I Introduction

Remarque

En fixant les noeuds (distincts), la condition avec p=s représente un système linéaire pour

Comme la matrice dans la formule est inversible (matrice de Vandermonde), la résolution de ce système nous donne une formule de quadrature d'ordre p = s.
Si l'on vérifie les conditions pour la formule de Simpson, on fait une observation intéressante: par définition, il est évident que la condition est satisfaite pour q = 1, 2, 3, mais on remarque qu'elle est aussi satisfaite pour q = 4. En effet:

Elle est donc d'ordre 4. Par conséquent, elle n'est pas seulement exacte pour les polynômes de degré 2 mais aussi pour les polynômes de degré 3. Ceci est est une propriété qui peut être généralisée aux formules de quadrature symétriques (c'est-à-dire ).

Coefficients et noeuds d'une formule de quadrature symétrique

Intégration numérique

II-8 Ordre

II-8-3 Remarque sur l'ordre

II-8-1 Définition

II-8 Ordre

II-8-4 Cas symétrique

I Introduction

Théorème

Une formule de quadrature symétrique a toujours un ordre pair: si elle est exacte pour les polynômes de degré , elle est exacte pour les polynômes de degré .

Chaque polynôme g(t) de degré peut être écrit sous la forme

où h(t) est un polynôme de degré et où c est une constante. Il suffit alors de montrer que la formule symétrique est exacte pour . A cause de la symétrie de cette fonction, la valeur exacte vaut

Pour une formule de quadrature symétrique on a

Donc l'approximation numérique de est également nulle.

II-8 Ordre

II-8-4 Cas symétrique

II-8-1 Définition

II-8-4 Cas symétrique

III Mise en oeuvre sur Matlab

III Mise en oeuvre sur Matlab

I Introduction

Intégration numérique

III Mise en oeuvre sur Matlab

III-1 Notations

III-1 Notations

I Introduction

Ici nous allons exécuter sur Matlab quelques méthodes de quadrature classiques pour approcher la valeur de l'intégrale

avec une subdivision de l'intervalle correspondante à

Intégration numérique

III-1 Notations

III-2 Méthode des rectangles à gauche

III-2 Méthode des rectangles à gauche

I Introduction

On note l'approximation de par la méthode des rectangles à gauche et l'erreur commise. Voici un programme Matlab qui calcule et :

 
%%%%%%%%%%%%%%%%%%%%%%%%
%      Donnees
%%%%%%%%%%%%%%%%%%%%%%%%
Iexa = log(2);
alpha = 1;
beta = 2;
N = 4;
h = (beta - alpha)/N;
x = [alpha:h:beta];
f = inline('1/x','x');
%%%%%%%%%%%%%%%%%%%%%%%%
% Corps du programme
%%%%%%%%%%%%%%%%%%%%%%%%
Irg = 0.0;
for i = 1:N
    Irg = Irg + h*f(x(i));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%
% Affichage des resultats
%%%%%%%%%%%%%%%%%%%%%%%%%%
Irg   
Erg = abs(Iexa - Irg) 
%%%%%%%%%%%%%%%%%%%%%%%%

Les résultats obtenus par ce programme sont:

 
Irg = 7.595238095e-01
Erg = 6.637662896e-02

III-2 Méthode des rectangles à gauche

III-1 Notations

III-3 Méthode des trapèzes

III-3 Méthode des trapèzes

I Introduction

On note l'approximation de par la méthode des trapèzes et l'erreur commise. Voici un programme Matlab qui calcule et :

 
%%%%%%%%%%%%%%%%%%%%%%%%
%      Donnees
%%%%%%%%%%%%%%%%%%%%%%%%
Iexa = log(2);
alpha = 1;
beta = 2;
N = 4;
h = (beta - alpha)/N;
x = [alpha:h:beta];
f = inline('1/x','x');
%%%%%%%%%%%%%%%%%%%%%%%%
% Corps du programme
%%%%%%%%%%%%%%%%%%%%%%%%
Itr = 0.0;
for i = 1:N
    Itr = Itr + h*(0.5*f(x(i)) + 0.5*f(x(i+1)));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%
% Affichage des resultats
%%%%%%%%%%%%%%%%%%%%%%%%%%
Itr   
Etr = abs(Iexa - Itr)

Les résultats obtenus par ce programme sont:

 
Itr = 6.970238095e-01
Etr = 3.876628964e-03

III-3 Méthode des trapèzes

III-1 Notations

III-4 Méthode de Simpson

III-4 Méthode de Simpson

I Introduction

On note l'approximation de par la méthode de Simpson et l'erreur commise. Voici un programme Matlab qui calcule et :

 
%%%%%%%%%%%%%%%%%%%%%%%%
%      Donnees
%%%%%%%%%%%%%%%%%%%%%%%%
Iexa = log(2);
alpha = 1;
beta = 2;
N = 4;
h = (beta - alpha)/N;
x = [alpha:h:beta];
f = inline('1/x','x');
%%%%%%%%%%%%%%%%%%%%%%%%
% Corps du programme
%%%%%%%%%%%%%%%%%%%%%%%%
Isi = 0.0;
for i = 1:N
Isi = Isi+h*(1/6*f(x(i))+2/3*f((x(i)+x(i+1))/2)+1/6*f(x(i+1)));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%
% Affichage des resultats
%%%%%%%%%%%%%%%%%%%%%%%%%%
Isi   
Es = abs(Iexa - Isi)

Les résultats obtenus par ce programme sont:

 
Isi = 6.931545307e-01
Esi = 7.350094585e-06

III-4 Méthode de Simpson

III-1 Notations

III-5 Commentaires des résultats

I Introduction

On voit bien que l'erreur absolue obtenue par la méthode de Simpson est beaucoup plus faible que celles obtenues par les deux autres. Ceci confirme la règle: plus l'ordre de la méthode est grand, plus la précision est bonne .

Intégration numérique

III-5 Commentaires des résultats

III-1 Notations

IV Etude de l'erreur d'une méthode de quadrature

IV Etude de l'erreur d'une méthode de quadrature

I Introduction

Pour étudier l'erreur commise en approchant une intégrale par l'une des formules de quadrature, nous commençons par une expérience numérique :

Intégration numérique

IV Etude de l'erreur d'une méthode de quadrature

IV-1 Expérience numérique

IV-1 Expérience numérique

IV-1-1 Nombre d'évaluation

IV-1-1 Nombre d'évaluation

I Introduction

Prenons une fonction f définie sur , subdivisons l'intervalle en plusieurs sous-intervalles équidistants ( ) et appliquons l'une des formules de quadrature du paragraphe précédent. Ensuite, étudions l'erreur (en échelle logarithmique),

en fonction du nombre d'évaluations f_e de la fonction f pour Newton-Cotes : f_e est défini par:

f_e = N(s-1) + 1

Le nombre f_e repésente une mesure pour le travail effectué par l'ordinateur.

Intégration numérique

IV-1-1 Nombre d'évaluation

IV-1-2 Exemple

IV-1-2 Exemple

IV-1-2 Exemple

I Introduction

Voici les résultats obtenus par les formules de Newton-Cotes (trapèzes, Simpson, Boole) pour l'int'grale

clear all;
Iexa = sin(2);
alpha = 0;
beta = 2;
f = inline('cos(x)','x');
%--------------------------
%--------------------------
% Méthode des trap`ezes
%--------------------------
%--------------------------
s = 2;
for j = 1:1:10 
%%%%%%%%%%%%%%%%%%%%%%%%
%      Donnees
%%%%%%%%%%%%%%%%%%%%%%%%
N = 2^j;
fetr(j) = log10(N*(s-1) +1);
h = (beta - alpha)/N;
x = [alpha:h:beta];
%%%%%%%%%%%%%%%%%%%%%%%%
% Corps du programme
%%%%%%%%%%%%%%%%%%%%%%%%
Itr=0.0;
for i = 1:N
Itr = Itr + h*(1/2*f(x(i)) + 1/2*f(x(i+1)));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%
% Affichage des resultats
%%%%%%%%%%%%%%%%%%%%%%%%%%
Etr(j) = log10(abs(Iexa - Itr)) ;
end
%--------------------------
%--------------------------
% Méthode de Simpson
%--------------------------
%--------------------------
s = 3;
for j=1:1:10 
%%%%%%%%%%%%%%%%%%%%%%%%
%      Donnees
%%%%%%%%%%%%%%%%%%%%%%%%
N = 2^j;
fesi(j) = log10(N*(s-1) +1);
h = (beta - alpha)/N;
x = [alpha:h:beta];
%%%%%%%%%%%%%%%%%%%%%%%%
% Corps du programme
%%%%%%%%%%%%%%%%%%%%%%%%
Isi = 0.0;
for i = 1:N
Isi = Isi+h*(1/6*f(x(i))+2/3*f((x(i)+x(i+1))/2)+1/6*f(x(i+1)));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%
% Affichage des resultats
%%%%%%%%%%%%%%%%%%%%%%%%%%
Esi(j) = log10(abs(Iexa - Isi)) ;
end
%--------------------------
%--------------------------
% Méthode de Boole (s=6)
%--------------------------
%--------------------------
s = 6;
for j = 1:1:8 
%%%%%%%%%%%%%%%%%%%%%%%%
%      Donnees
%%%%%%%%%%%%%%%%%%%%%%%%
N = 2^j;
febo(j) = log10(N*(s-1) +1);
h = (beta - alpha)/N;
x = [alpha:h:beta];
%%%%%%%%%%%%%%%%%%%%%%%%
% Corps du programme
%%%%%%%%%%%%%%%%%%%%%%%%
Ibo = 0.0;
for i = 1:N
Ibo = Ibo + h*(19/288*f(x(i)) + 75/288*f(x(i)+h/5) + 
50/288*f(x(i)+(2*h/5)) + 50/288*f(x(i)+ (3*h/5)) + 
75/288*f(x(i)+ (4*h/5)) + 19/288*f(x(i+1)));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%
% Affichage des resultats
%%%%%%%%%%%%%%%%%%%%%%%%%%
Ebo(j) = log10(abs(Iexa - Ibo)) ;
plot(fetr, Etr, 'k-.', fesi, Esi, 'k-+', febo, Ebo, 'k-*')
legend('Trap`ezes', 'Simpson', 'Boole (s=6)')
xlabel('log10(Erreur)');
ylabel('log10(fe)');
title('Le travail fe en fonction de l''erreur');
end

La figure ci-dessous montre donne les résultats pour

IV-1-2 Exemple

IV-1-1 Nombre d'évaluation

IV-1-2 Exemple

IV-1-3 Interprétation des résultats

IV-1-3 Interprétation des résultats

I Introduction

Nous constatons que:

dépend linéairement du nombre de chiffres exacts, donné par .
La pente de chaque droite est où p est l'ordre de la méthode de quadrature.
Pour un travail équivalent (même f_e), les formules avec un ordre élevé ont une meilleure précision.

Intégration numérique

IV-1-3 Interprétation des résultats

IV-1-1 Nombre d'évaluation

IV-1-2 Exemple

IV-1-4 Justification des résultats

I Introduction

Etudions d'abord l'erreur faite sur un sous-intervalle de longueur h.

On considère la formule de quadrature d'ordre p. En supposant que f est suffisament différentiable, on peut remplacer f(x₀ + t h) et f(x₀ + c_i h) par les séries de Taylor au voisinage de x₀:

La constante définie par

s'appelle constante de l'erreur. Si on suppose que h est assez petit pour négliger devant , on obtient:

Cette formule nous permet de mieux comprendre les résultats de la figure précédente. En effet, on peut écrire et . Par conséquent,

Ceci montre la dépendance linéaire entre et et le fait que la pente soit de .

Intégration numérique

IV-1-4 Justification des résultats

IV-1-1 Nombre d'évaluation

IV-1-2 Exemple

IV-2 Estimation rigoureuse de l'erreur

IV-2 Estimation rigoureuse de l'erreur

IV-2-1 Noyau de Peano

IV-2-1 Noyau de Peano

I Introduction

Dans ce paragraphe on s'occupe de l'estimation exacte de l'erreur d'une formule de quadrature en vue de démontrer les théorèmes de convergence et assurer une certaine précision du résultat numérique.

Théorème [et Définition]

Soit une formule de quadrature d'ordre p et un entier k vérifiant . Considérons une fonction de classe , alors l'erreur définie par la formule vérifie:

où N_k est le noyau de Peano , défini par:

La formule de Taylor avec reste intégral appliquée à f au point x₀ donne:

En combinant cette dernière formule avec la formule et en utilisant le fait que

et en remarquant que la partie polynomiale dans l'avant-dernière équation ne contribue pas à l'erreur (à cause que ), nous obtenons:

Une évaluation de l'intégrale intérieure donne le résultat.

Remarque

Pour une formule de quadrature d'ordre p et un entier k vérifiant on a:

où C est la constante de l'erreur définie par la formule .

Exemple

Les noyaux de Peano pour la méthode du point milieu sont donnés par:

IV-2-2 Majoration de l'erreur

IV-2-1 Noyau de Peano

IV-2-2 Majoration de l'erreur

I Introduction

Nous sommes maintenant en mesure d'estimer l'erreur commise pour l'intervalle tout entier et ceci pour une subdivision arbitraire . Rappelons que, comme dans la formule , l'erreur est donnée par:

On a alors le théorème suivant:

Théorème

Soit une formule de quadrature d'ordre p et un entier k vérifiant . Considérons une fonction de classe . Alors l'erreur E(f) définie par la formule vérifie l'estimation suivante:

où .

Pour la formule du point milieu, on a:

La formule donne:

Comme l'erreur est la somme des erreurs sur les sous-intervalles de la subdivision, nous obtenons:

et puisque , on obtient l'équation .

Exemple

Pour la formule des trapèzes:

Pour la formule de Simpson:

Pour la formule de Newton-Cotes ( s = 5):

Remarque

Le calcul de pour ces formules n'est pas difficile. Considérons par exemple la formule de Newton-Cotes avec s = 5. Nous constatons que N₆(s) ne change pas de signe sur et en utilisant la remarque , nous obtenons:

Noyau de Peano

IV-2-2 Majoration de l'erreur

IV-2-1 Noyau de Peano

IV-2-2 Majoration de l'erreur

V Exemples de calcul numérique de l'ordre

V Exemples de calcul numérique de l'ordre

I Introduction

Intégration numérique

V Exemples de calcul numérique de l'ordre

V-1 Préliminaires

V-1 Préliminaires

I Introduction

Ici nous allons vérifier à l'aide de Matlab l'ordre de quelques méthodes de quadrature déjà étudiées précédemment pour approcher la valeur de l'intégrale

avec

et une subdivision de plus en plus fine de l'intervalle correspondante à

Intégration numérique

V-1 Préliminaires

V-2 Méthode des rectangles à gauche

V-2 Méthode des rectangles à gauche

I Introduction

On note l'approximation de par la méthode des rectangles à gauche et l'erreur commise. On affiche les valeurs de j, , , , et . Code Matlab

 
clear all;
fid = 1;
fmt = '%% %10d  %20.9e     %20.9e   %20.9e     %20.9e n';
for j = 1:2:17
%%%%%%%%%%%%%%%%%%%%%%%%
%      Donnees
%%%%%%%%%%%%%%%%%%%%%%%%
N = 2^j;
Iexa = log(2);
alpha = 1;
beta = 2;
h = (beta - alpha)/N;
x = [alpha:h:beta];
f = inline('1/x','x');
%%%%%%%%%%%%%%%%%%%%%%%%
% Corps du programme
%%%%%%%%%%%%%%%%%%%%%%%%
Irg = 0.0;
for i = 1:N
Irg = Irg + h*f(x(i));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%
% Affichage des resultats
%%%%%%%%%%%%%%%%%%%%%%%%%%
%Irg
Erg = abs(Iexa - Irg) ;
Erg1 = abs(Iexa - Irg)/h ;
Erg2 = abs(Iexa - Irg)/h^2 ;
%%%%%%%%%%%%%%%%%%%%%%%%
fprintf(fid, fmt, j, Irg, Erg, Erg1, Erg2);
end

Les résultats obtenus par ce programme sont:

j Irg Erg Erg/h Erg/h^2

1 8.333333333e-01 1.401861528e-01 2.803723055e-01 5.607446111e-01 3 7.253718504e-01 3.222466981e-02 2.577973585e-01 2.062378868e+00 5 7.010207083e-01 7.873527709e-03 2.519528867e-01 8.062492374e+00 7 6.951041202e-01 1.956939668e-03 2.504882775e-01 3.206249952e+01 9 6.936357002e-01 4.885196685e-04 2.501220703e-01 1.280625000e+02 11 6.932692658e-01 1.220852137e-04 2.500305176e-01 5.120625000e+02 13 6.931776991e-01 3.051850945e-05 2.500076294e-01 2.048062500e+03 15 6.931548100e-01 7.629452736e-06 2.500019072e-01 8.192062496e+03 17 6.931490879e-01 1.907352286e-06 2.500004788e-01 3.276806276e+04

Commentaires:

On constate que se stabilise autour de 2.5e-01 alors que explose au fur et à mesure que j augmente (les subdivisions de plus en plus fines). Ceci confirme le fait que cette méthode est d'ordre 1.

V-2 Méthode des rectangles à gauche

V-1 Préliminaires

V-3 Méthode des trapèzes

V-3 Méthode des trapèzes

I Introduction

On note l'approximation de par la méthode des trapèzes et l'erreur commise. On affiche les valeurs de j, , , , , et .

j Itr Etr Etr/h Etr/h^2 Etr/h^3

 
clear all;
fid = 1;
fmt = '%% %10d  %12.9e     %12.9e   %12.9e   %12.9e     %12.9e n';
for j = 1:2:17
%%%%%%%%%%%%%%%%%%%%%%%%
%      Donnees
%%%%%%%%%%%%%%%%%%%%%%%%
N = 2^j;
Iexa = log(2);
alpha = 1;
beta = 2;
h = (beta - alpha)/N;
x = [alpha:h:beta];
f = inline('1/x','x');
%%%%%%%%%%%%%%%%%%%%%%%%
% Corps du programme
%%%%%%%%%%%%%%%%%%%%%%%%
Itr = 0.0;
for i = 1:N
Itr = Itr + h*(0.5*f(x(i)) + 0.5*f(x(i+1)));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%
% Affichage des resultats
%%%%%%%%%%%%%%%%%%%%%%%%%%
Etr = abs(Iexa - Itr) ;
Etr1 = abs(Iexa - Itr)/h ;
Etr2 = abs(Iexa - Itr)/h^2 ;
Etr3 = abs(Iexa - Itr)/h^3 ;
%%%%%%%%%%%%%%%%%%%%%%%%
fprintf(fid, fmt, j, Itr, Etr, Etr1 , Etr2, Etr3);
end

Les résultats obtenus par ce programme sont:

1 7.08333e-01 1.51862e-02 3.03723e-02 6.07446e-02 1.21489e-01 3 6.94122e-01 9.74670e-04 7.79736e-03 6.23789e-02 4.99031e-01 5 6.93208e-01 6.10277e-05 1.95289e-03 6.24924e-02 1.99976e+00 7 6.93151e-01 3.81467e-06 4.88278e-04 6.24995e-02 7.99994e+00 9 6.93147e-01 2.38418e-07 1.22070e-04 6.25000e-02 3.20000e+01 11 6.93147e-01 1.49012e-08 3.05176e-05 6.25000e-02 1.28000e+02 13 6.93147e-01 9.31321e-10 7.62938e-06 6.24999e-02 5.11999e+02 15 6.93147e-01 5.82108e-11 1.90745e-06 6.25033e-02 2.04811e+03 17 6.93147e-01 3.63654e-12 4.76648e-07 6.24752e-02 8.18875e+03

Commentaires:

On constate que se stabilise autour de 6.25e-02 alors que explose au fur et à mesure que j augmente. Ceci confirme le fait que cette méthode est d'ordre 2.

V-3 Méthode des trapèzes

V-1 Préliminaires

V-4 Méthode de Simpson

I Introduction

On note l'approximation de par la méthode de Simpson et l'erreur commise. On affiche les valeurs de j, , , , , et .

j Isi Esi Esi/h^3 Esi/h^4 Esi/h^5

 
clear all;
fid = 1;
fmt = '%% %3d  %12.5e  %12.5e  %12.5e  %12.5e  %12.5e n';
for j = 1:1:10
%%%%%%%%%%%%%%%%%%%%%%%%
%      Donnees
%%%%%%%%%%%%%%%%%%%%%%%%
N = 2^j;
Iexa = log(2);
alpha = 1;
beta = 2;
h = (beta - alpha)/N;
x = [alpha:h:beta];
f = inline('1/x','x');
%%%%%%%%%%%%%%%%%%%%%%%%
% Corps du programme
%%%%%%%%%%%%%%%%%%%%%%%%
Isi = 0.0;
for i = 1:N
Isi = Isi + h*(1/6*f(x(i)) + 2/3*f((x(i) + x(i+1))/2) + 1/6*f(x(i+1)));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%
% Affichage des resultats
%%%%%%%%%%%%%%%%%%%%%%%%%%
Esi = abs(Iexa - Isi) ;
Esi3 = abs(Iexa - Isi)/h^3 ;
Esi4 = abs(Iexa - Isi)/h^4 ;
Esi5 = abs(Iexa - Isi)/h^5 ;
%%%%%%%%%%%%%%%%%%%%%%%%
fprintf(fid, fmt, j, Isi, Esi, Esi3 , Esi4, Esi5);
end

Les résultats obtenus par ce programme sont:

1 6.93254e-01 1.06788e-04 8.54302e-04 1.70860e-03 3.41721e-03 2 6.93155e-01 7.35009e-06 4.70406e-04 1.88162e-03 7.52650e-03 3 6.93148e-01 4.72259e-07 2.41797e-04 1.93437e-03 1.54750e-02 4 6.93147e-01 2.97299e-08 1.21774e-04 1.94838e-03 3.11740e-02 5 6.93147e-01 1.86151e-09 6.09979e-05 1.95193e-03 6.24619e-02 6 6.93147e-01 1.16398e-10 3.05130e-05 1.95283e-03 1.24981e-01 7 6.93147e-01 7.27574e-12 1.52583e-05 1.95307e-03 2.49992e-01 8 6.93147e-01 4.54081e-13 7.61822e-06 1.95026e-03 4.99268e-01 9 6.93147e-01 2.80886e-14 3.76999e-06 1.93024e-03 9.88281e-01 10 6.93147e-01 2.66454e-15 2.86102e-06 2.92969e-03 3.00000e+00

Commentaires:

On constate que se stabilise autour de 1.95e-03 alors que explose au fur et à mesure que j augmente. Ceci confirme le fait que cette méthode est d'ordre 4.

V-4 Méthode de Simpson

V-1 Préliminaires

VI Bibliographie

VI Bibliographie

I Introduction

VI Bibliographie

Philipe G. Ciarlet. Introduction à l'analyse numérique et à l'optimisation . Dunod 1990.
Jean-Pierre Demailly. Analyse numérique et équations différentielles . Presses Universitaires de Grenoble, 1996.
Ernst Hairer. Introduction à l'analyse numérique . Université de Genève, section mathématiques, case postale 240. Octobre 2001.

Intégration numérique

VI Bibliographie

VII Exercices

VII Exercices

I Introduction

VII Exercices

Soit une fonction de classe . On considère la méthode d'intégration numérique approchée donnée par

Calculer l'ordre de cette méthode en fonction de w.
On se place dans le cas où cette méthode est d'ordre 1.
1. Calculer le noyau de Peano G₁(t) et tracer le graphe de G₁ pour . Pour quelles valeurs de w le noyau G₁ est-il de signe constant?
2. Montrer que l'erreur vérifie la majoration
  
  où C(w) est une constante dont on déterminera la valeur optimale
  1. lorsque G₁ est de signe constant.
  2. lorsque .

On rappelle que par construction, les méthodes de Newton-Cotes sont les formules de quadratures élémentaires de type

telles que les noeuds soient équidistants et centrés dans l'intervalle , les étant choisis de telle façon que ces formules soient exactes pour tout polynôme P de degré inférieur ou égale à n. Montrer que si n est pair ces formules sont aussi exactes pour les polynômes de degré n+1. (Indication : on pourra remarquer que et en tirer les conséquences pour les polynômes impairs.)

Construire les formules d'intégration numérique suivantes :

Déterminer leur noyau de Peano et en déduire l'erreur commise.

Montrer que

(Indication : appliquer la formule d'Euler-MacLaurin à entre 0 et 1.)
Montrer que si est une fonction périodique de période b-a, alors

et où T_h(f) représente l'évaluation de la formule des trapèzes de pas h pour f sur

Soient x₁ et x₂ deux points de et et . On considére la formule d'itégration suivante :

Quelles conditions doivent vérifier et pour que cette formule soit exacte pour

les fonctions constantes?
les fonctions affines?
les polynômes de degré inférieur ou égale à 2?

On considère la formule d'intégration suivante :

Déterminer les valeurs de et 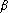pour que (1) soit exacte sur .
En déduire les valeurs de et 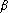pour que (1) soit d'ordre le plus élevé possible.
1. Calculer le noyau de Peano dans le cas où (1) est d'ordre 3 et vérifier que ce noyau est une fonction paire.
2. En déduire qu'il existe tel que où E(f) est l'erreur d'intégration.
3. Donner la formule d'intégration relative à (1) sur
4. Estimer l'erreur d'intégration obtenue par la méthode composée associée à (1) sur avec un pas constant .

On considére la formule d'intégration suivante :

Déterminer et x₂ de sorte que cette formule soit exacte sur .
Calculer alors l'ordre de cette méthode.

Soit . Montrer qu'il existe un polynôme P unique de degré 2 vérifiant:

Déterminer et la comparer à .
On considére . On veut calculer cette intégrale avec une erreur inférieur à .
1. Déterminer le pas h nécessaire pour la méthode des trapèzes.
2. Déterminer le pas h nécessaire pour la méthode de Simpson.

Trouver l'ordre des formule de : rectangle, trapèze et Simpson.
Pour . On pose

Montrer que .
En déduire . Calculer par deux méthodes différentes .
Enoncer le thérème de Peano et montrer que si alors on a :