Cours/TD d'algèbre linéaire
Algèbre linéaire
|
| Réalisé sous WIMS dans le cadre du CAMPUS ESCALES, avec le soutien de l'UFR Sciences de Nice et de l'IUFM de Nice |
-
Quelques rappels sur les espaces vectoriels
-
Séance 1 - durée 1h30
-
Séance 2 - durée 1h30
-
Espaces vectoriels de dimension finie
-
Séance 3 - durée 1h30
-
Séance 4 - durée 1h30
-
Formes linéaire - dualité
-
Séance 5 - durée 1h30
-
Séance 6 - durée 1h30
-
Matrice d'une application linéaire
-
Séance 7 - durée 1h30
-
Séance 8 - durée 1h30
-
Applications multilinéaires - Déterminants
-
Séance 9 - durée 1h30
-
Séance 10 - durée 1h30
-
Réduction des endomorphismes et des matrices carrées
-
Séance 11 - durée 1h30
-
Séance 12 - durée 1h30
-
Séance 13 - durée 1h30
-
Séance 14- durée 1h30
-
Séance 15 - durée 1h30
-
Des Exos Inter-Actifs avec WIMS
Exercice sur les notions "Espaces/Sous-espaces vectoriels"
Exercice sur les matrices de trace nulle
|
|
|
|
|
|
| Exercice sur les notions "Espaces/Sous-espaces vectoriels" |
| Exercice sur les matrices de trace nulle |
| Modules d'exercices | Exercices sur les endomorphismes d'espaces vectoriels |
|---|---|
| Exercices sur la réduction des endomorphismes d'espaces vectoriels |
Conformément au programme,
|
Session 1
Feuille de Travail 1
| Petite séance d'entraînement avec WIMS |
- est-il un sous-espace vectoriel de ?
- Soient
et
.
- a)
- Vérifier que
est un
sous-espace vectoriel
de
.
A i d e ? Oui
- b)
- Pour , donner une base de .
- c)
- On suppose . Soit (resp. ) un supplémentaire de (resp. ) dans . est-il un supplémentaire de ? Donner une base d'un supplémentaire de .
| prendre cette séance WIMS |
On considère . est-il un sous-espace vectoriel de
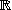 3?
Même question pour
.
3?
Même question pour
.
| Passer à la Feuille de Travail 2 |
| ou retourner au Sommaire |
Feuille de Travail 2
- L'ensemble des applications linéaires de E dans F est un K- espace vectoriel . Lorsque E=F on parle d'endomorphismes de E.
- L'espace des endomorphismes de
E,
EndK(E) muni de la loi de composition
des applications est
une
K-algèbre.
Faites en la vérification après avoir rappelé la définition d'une K-algèbre.A i d e ? Oui - Soit
f:E
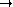 F une
application linéaire
bijective. Alors
est
linéaire
. On dit alors que les deux
K-
espaces vectoriels
E et
F sont isomorphes. Lorsque
E=F, on
parle d'automorphisme de
E.
F une
application linéaire
bijective. Alors
est
linéaire
. On dit alors que les deux
K-
espaces vectoriels
E et
F sont isomorphes. Lorsque
E=F, on
parle d'automorphisme de
E.
- L'ensemble des automorphismes de
E (
Aut(E)) muni de la loi de
composition des applications est un groupe.
Faites en la vérification après avoir rappelé la définition d'un groupe.A i d e ? Oui
 E,
l'application linéaire
définie par
f(x1,x2)=x1+x2. Montrer que
Ker(f)
est isomorphe à
E1
E,
l'application linéaire
définie par
f(x1,x2)=x1+x2. Montrer que
Ker(f)
est isomorphe à
E1  E2.
E2.
 EndK(E) est un projecteur si
p2=p (
).
Montrer que si
p
EndK(E) est un projecteur si
p2=p (
).
Montrer que si
p  EndK(E) est un projecteur, alors on a
. La réciproque est-elle vraie?
EndK(E) est un projecteur, alors on a
. La réciproque est-elle vraie?
- Soient
E un
K-
espace vectoriel
,
une famille finie d'éléments
de
E. On dit que la famille
est libre
(ou linéairement indépendante) si
la relation (  i
i  K)
K)
entraîne .S'il existe non tous nuls tels que , la famille est dite liée. - Une famille quelconque d'éléments de E est dite libre si toute sous-famille finie de est libre.
- Si est une famille génératrice et libre, on dit que est une base de E.

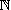 2, calculer
.
En déduire que la famille
est libre dans le
2, calculer
.
En déduire que la famille
est libre dans le
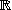 -espace des fonctions
rélles de classe
sur
-espace des fonctions
rélles de classe
sur
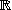 .
.
| Passer à la Feuille de Travail 3 |
| ou retourner au Sommaire |
Session 2
Feuille de Travail 3
Collection de définitions et résultats fondamentaux sur
les
espaces vectoriels
de dimension finie.
- A SAVOIR -
- est une base de E
- est une partie génératrice minimale (pour la relation d'inclusion)
- est une partie libre maximale.
Alors on a n
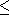 p.
p.
Soient E un K-espace de dimension finie, une partie génératrice finie de E et une partie libre .
Alors il existe base de E telle que
Soient E un K-espace de dimension finie, une partie libre finie, une partie génératrice finie de E.
Alors il existe tel que est une base de E.
E étant un K- espace vectoriel de dimension finie, toutes les bases de E ont même nombre d'éléments. Ce nombre est appelé dimension de E.
Soient E un K- espace vectoriel , une famille de vecteurs de E. On appelle rang de , noté , la dimension (supposée finie) du sous-espace vectoriel de E engendré par .
| Passer à la Feuille de Travail 4 |
| ou retourner au Sommaire |
Feuille de Travail 4
Soient E, F deux K- espaces vectoriels , f: E
 F une
application linéaire
. On suppose que
E est de
dimension
finie.
F une
application linéaire
. On suppose que
E est de
dimension
finie.
On appelle rang de f, noté rg(f), la dimension du sous-espace vectoriel Im(f)
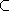 F de
F.
F de
F.
 EndK(E) un
endomorphisme
de
E.
Montrer que
Im(f)=Im(f2) entraîne
.
La réciproque est-elle vraie?
EndK(E) un
endomorphisme
de
E.
Montrer que
Im(f)=Im(f2) entraîne
.
La réciproque est-elle vraie?
 F deux
applications linéaires
.
F deux
applications linéaires
.
- Comparer rg(f+g) et (rg(f)+rg(g)).
- Montrer que .
 EndK(V) est dit nilpotent s'il existe un entier
p>1 tel que
up=0. Le plus petit entier naturel non nul
r
vérifiant
ur=0 est appelé indice de nilpotence de
u.
EndK(V) est dit nilpotent s'il existe un entier
p>1 tel que
up=0. Le plus petit entier naturel non nul
r
vérifiant
ur=0 est appelé indice de nilpotence de
u.
- Montrer que si
V est de
dimension
finie
d et
u
 EndK(V) est
un
endomorphisme
nilpotent, alors on a
ud=0.
EndK(V) est
un
endomorphisme
nilpotent, alors on a
ud=0.
- Donner des exemples d'endomorphismes nilpotents (avec différents indices de nilpotence) d'un K- espace vectoriel V de dimension 4.
- Soit u un endomorphisme nilpotent d'un K- espace vectoriel V de dimension d>0. r étant l'indice de nilpotence de u, on considère e(u) le sous-espace vectoriel de EndK(V) engendré par . Donner une base de e(u).
- On note IdV l'endomorphisme identité de V. Montrer que si u est nilpotent, alors pour tout entier naturel s, (IdV-u)s est un automorphisme de V.
- Soit
u un
endomorphisme
nilpotent d'un
K-
espace vectoriel
V de
dimension
d>0.
r étant l'indice de nilpotence de
u, on
considère
x
 V vérifiant
.
Montrer que la famille
V vérifiant
.
Montrer que la famille
Donner un exemple pour dimK(V)=4.
| Passer à la Feuille de Travail 5 |
| ou retourner au Sommaire |
Session 3
Feuille de Travail 5
Soit E un K- espace vectoriel . On appelle forme linéaire sur E, toute application linéaire f: E
 K. L'ensemble
des formes linéaires sur
E a une structure de
K-
espace vectoriel
appelé
espace vectoriel
dual de
E et est
noté
.
Le dual de
est appelé bidual de
E et est noté
K. L'ensemble
des formes linéaires sur
E a une structure de
K-
espace vectoriel
appelé
espace vectoriel
dual de
E et est
noté
.
Le dual de
est appelé bidual de
E et est noté
Soit E un K- espace vectoriel . On appelle hyperplan de E tout supplémentaire d'une droite vectorielle de E.
- Soient E un K- espace vectoriel et une forme linéaire non nulle sur E. Montrer que Ker(f) est un hyperplan de E.
- Montrer que tout hyperplan
H d'un
K-
espace vectoriel
E est le noyau d'une
forme linéaire
f: E
 K.
L'équation
f(x)=0 est alors appelée équation de l'hyperplan
H.
K.
L'équation
f(x)=0 est alors appelée équation de l'hyperplan
H.
Montrer que ev est linéaire injective.
forment une base de appelée base duale de la base .
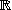 -
espace vectoriel
des polynômes à
une variable à coefficients dans
-
espace vectoriel
des polynômes à
une variable à coefficients dans
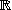 . On prend pour
base
de
E le
système
et on considère la
famille
définie par
. On prend pour
base
de
E le
système
et on considère la
famille
définie par
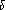 ij
ij
Montrer que la famille est libre . Cette famille constitue-t-elle une base de ?
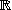 -
espace vectoriel
des
polynômes à une variable à coefficients dans
-
espace vectoriel
des
polynômes à une variable à coefficients dans
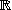 et de
degré au plus
n. On considère la famille
définie
par
et de
degré au plus
n. On considère la famille
définie
par
Vérifier que est une base de et déterminer la base de E dont elle est la duale.
- On dit que
x
 E est orthogonal à
(ou que
est orthogonal à
x
E est orthogonal à
(ou que
est orthogonal à
x  E) si
f(x)=0.
E) si
f(x)=0.
- On dit qu'une partie non vide
est orthogonale à
une partie non vide
si pour tout
x
 A et tout
on a
f(x)=0.
A et tout
on a
f(x)=0.
| Passer à la Feuille de Travail 6 |
| ou retourner au Sommaire |
Feuille de Travail 6
- Soit A une partie non vide de E. Alors l'ensemble des formes linéaires orthogonales à A est un sous-espace vectoriel de .
- Soient A une partie non vide de E et Vect(A) le sous-espace vectoriel de E engendré par A. Alors on a .
- Enoncés analogues pour une partie non vide B de .
Soit E un K- espace vectoriel de dimension finie n.
- Pour tout
sous-espace vectoriel
V de
E,
on a
- Pour tout
sous-espace vectoriel
W de
,
on a
Preuve: Exercice.
Soit E un K- espace vectoriel de dimension finie n, son dual.
- Pour tout sous-espace vectoriel V de E, on a .
- Pour tout sous-espace vectoriel W de , on a .
- .
- .
Soient E et F deux K- espaces vectoriels et f: E
 F une
application linéaire
. Pour toute forme linéaire
,
on a
. L'application
définie par
est
linéaire
et est appelée transposée de
f.
Pour tout
x
F une
application linéaire
. Pour toute forme linéaire
,
on a
. L'application
définie par
est
linéaire
et est appelée transposée de
f.
Pour tout
x  E,
.
E,
.
- L'application qui à f associe est linéaire .
- Pour tout
et tout
,
on a
- Si
est bijective, il en est de même de
et
on a
- Si
E et
F sont des
K-
espaces vectoriels
de
dimensions
finies, alors
l'application
qui à
f associe
est un
isomorphisme
et on a
| Passer à la Feuille de Travail 7 |
| ou retourner au Sommaire |
Session 4
Feuille de Travail 7
Matrice d'une application linéaire
Tous les
espaces vectoriels
considérés dans ce paragraphe seront
supposés de
dimension
finie. Le
corps
de base est toujours un sous-corps
de
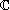 .
.
 F une
application linéaire
. Tout
x
F une
application linéaire
. Tout
x  E,
s'écrit de manière unique
E,
s'écrit de manière unique
 K.
K.
On a donc
et l'application linéaire f est entièrement déterminée par la donnée des f(ej), .
Comme est une base de F, pour tout , on a de manière unique
L'application linéaire f est donc entièrement déterminée par la donnée des p×n scalaires .
On appelle matrice de l'application linéaire f: E
 F relativement aux
bases
et
,
la matrice à coefficients dans
K
F relativement aux
bases
et
,
la matrice à coefficients dans
K
Les coordonnées dans la base du vecteur f(ej) se trouvent sur la j-ème colonne de la matrice ci-dessus.
Soient E, F deux K- espaces vectoriels de dimensions finies respectives n et p, munis respectivement des bases et . Soit f: E
 F une
application linéaire
.
F une
application linéaire
.
- Si n=1, est une matrice unicolonne.
- Si p=1, est une matrice uniligne.
- Si E=F, on a n=p, f est un endomorphisme de E et est une matrice carrée n×n. Si en plus , est notée tout simplement et on parle de la matrice de l'endomorphisme f dans la base .
On considère les
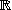 -
espaces vectoriels
et
munis respectivement des
bases
et
.
Soit
f: E
-
espaces vectoriels
et
munis respectivement des
bases
et
.
Soit
f: E  F définie par
f(P)=P'. Déterminer
.
F définie par
f(P)=P'. Déterminer
.
Quelle est la matrice dans la base de l'endomorphisme g de F défini par g(P)= XP'?
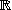 3 est supposé muni d'une
base orthonormée
. On note
(x,y,z)
les coordonnées d'un vecteur de
3 est supposé muni d'une
base orthonormée
. On note
(x,y,z)
les coordonnées d'un vecteur de
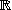 3 dans cette
base
. Donner dans
la
base
la matrice de chacune des transformations
linéaires
suivantes:
3 dans cette
base
. Donner dans
la
base
la matrice de chacune des transformations
linéaires
suivantes:
- La symétrie (orthogonale) par rapport au plan des (x,y)
- La symétrie (orthogonale) par rapport au plan d'équation x=y
- La projection orthogonale sur le plan d'équation y=z
| Exercice 1 avec WIMS |
| Exercice 2 avec WIMS |
| Exercice 3 avec WIMS |
| Exercice 4 avec WIMS |
| Passer à la Feuille de Travail 8 |
| ou retourner au Sommaire |
Feuille de Travail 8
 E, donnée par
f(P)= q(P)+r(P), où
q(P) est le quotient de la division de
P par
X, et
r(P) est le reste de
la division de
P par
Xn.
E, donnée par
f(P)= q(P)+r(P), où
q(P) est le quotient de la division de
P par
X, et
r(P) est le reste de
la division de
P par
Xn.
Montrer que f est un endomorphisme de E et donner la matrice M de f dans la base . Calculer le rang de M.
Soient E, F deux K- espaces vectoriels de dimensions finies, . Soient et deux bases de E, et deux bases de F. On pose
(la matrice faisant passer de la base à la base ),
(la matrice faisant passer de la base à la base ).
Soit tel que . Donner en fonction de M, P et Q.
- Montrer que la relation binaire
définie sur
par
est une relation d'équivalence sur .
Deux matrices M et sont dites équivalentes si
- Montrer que deux matrices M et sont équivalentes si et seulement si elles ont même rang .
- Montrer que la relation binaire
définie sur
Mn(K) par
est une relation d'équivalence sur Mn(K).
Deux matrices M et N Mn(K) sont dites semblables si
Mn(K) sont dites semblables si
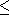 1 si et seulement si
1 si et seulement si
Soit une matrice carrée n×n à coefficients dans K. On appelle trace de M notée Tr(M) le scalaire
- Montrer que l'application
Tr: Mn(K)
 K qui à une matrice
carrée
n×n associe sa trace est une
forme linéaire
.
K qui à une matrice
carrée
n×n associe sa trace est une
forme linéaire
.
- Pour
M,
N
 Mn(K), montrer que
Mn(K), montrer que
Tr(MN)=Tr(NM)
- Montrer que deux matrices semblables ont même trace.
 Mn(K) de trace nulle est semblable à
une matrice dont tous les termes diagonaux sont nuls.
Mn(K) de trace nulle est semblable à
une matrice dont tous les termes diagonaux sont nuls.
| Pour commencer, vous pourrez chercher une preuve pour les matrices . Entraînez vous ensuite avec WIMS, puis dégagez l'idée d'une preuve pour une matrice carrée quelconque. |
| Exercice sur les matrices de trace nulle |
| Passer à la Feuille de Travail 9 |
| ou retourner au Sommaire |
Session 5
Feuille de Travail 9
Applications multilinéaires - Déterminants
Une application est dite n-linéaire si pour tout ,
quel que soit ,
l'application partielle est linéaire .
Lorsque F=K on parle de forme n-linéaire. Lorsque n=2 (resp. n=3) on parle d'application bilinéaire (resp. trilinéaire).
est bilinéaire.
Ne pas confondre et (l'espace des applications linéaires de l'espace vectoriel produit dans F).
 x).
x).
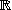 -
espace vectoriel
de
dimension
finie
m>0.
Calculer les
dimensions
des
-
espace vectoriel
de
dimension
finie
m>0.
Calculer les
dimensions
des
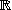 -
espaces vectoriels
suivants:
-
espaces vectoriels
suivants:
- et
- et
- et
- Rappeler la définition d'une forme n-linéaire symétrique sur E. Après avoir vérifier que l'ensemble des formes n-linéaires symétriques sur E est un K- espace vectoriel , calculer la dimension de l'espace vectoriel des formes bilinéaires symétriques sur E.
- Mêmes questions que ci-dessus pour ce qui concerne les formes n-linéaires antisymétriques sur E.
Soient E et F des K- espaces vectoriels . Une application n-linéaire
f: En
 F est dite alternée
si pour tout
on a:
F est dite alternée
si pour tout
on a:
En particulier si , on a
| Passer à la Feuille de Travail 10 |
| ou retourner au Sommaire |
Feuille de Travail 10
Applications multilinéaires - Déterminants
Soient E un K- espace vectoriel de dimension finie n et u un endomorphisme de E. Alors il existe un unique scalaire

 K tel que
pour toute
base
de
E on a
K tel que
pour toute
base
de
E on a
Ce scalaire
 s'appelle déterminant de
u et est noté
det(u).
s'appelle déterminant de
u et est noté
det(u).
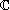 , on se donne
n
points
d'affixes respectifs
ai(1
, on se donne
n
points
d'affixes respectifs
ai(1 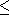 i
i 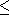 n).
n).
Etudier la possibilité de construire un polygone du plan affine, dont les Ai sont les milieux des côtés.
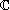 3 le système linéaire suivant où
t
3 le système linéaire suivant où
t 
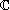 est un paramètre:
est un paramètre:
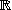 3 le système linéaire
suivant:
3 le système linéaire
suivant:
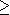 2) et
A
2) et
A  Mn(K), donner le rang de
com(A) (la comatrice de
A) en fonction de celui de
A.
Mn(K), donner le rang de
com(A) (la comatrice de
A) en fonction de celui de
A.
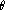 est un nombre réel fixé.
n est un entier naturel (
n
est un nombre réel fixé.
n est un entier naturel (
n 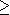 2). Calculer le déterminant de la matrice
définie par
2). Calculer le déterminant de la matrice
définie par
Même question pour la matrice définie par
| Passer à la Feuille de Travail 11 |
| ou retourner au Sommaire |
Session 6
Feuille de Travail 11
Réduction des endomorphismes et des matrices carrées
6.1 Sous-espaces stables par un endomorphisme
 , à domaine
K). On dit
que
E a une structure de
K-algèbre
est une
K-algèbre)
si:
, à domaine
K). On dit
que
E a une structure de
K-algèbre
est une
K-algèbre)
si:
- (E,+, ×) est un K- espace vectoriel
- est un anneau
- Pour tout

 K et tout couple
(x,y) d'éléments
de
E on a
K et tout couple
(x,y) d'éléments
de
E on a
On dit que E a une structure de K-algèbre unitaire si l'anneau admet un élément neutre pour la multiplication interne.
Soit
E un
K-
espace vectoriel
.
EndK(E) est le
K-
espace vectoriel
des
applications linéaires
u: E  E.
est une
K-algèbre.
E.
est une
K-algèbre.
Soient E un K- espace vectoriel (de dimension quelconque), V un sous-espace vectoriel de E et u
 EndK(E). On dit que
V est stable par
u si
u(V)
EndK(E). On dit que
V est stable par
u si
u(V) 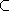 V
(i.e. pour tout
x
V
(i.e. pour tout
x  V, on a
u(x)
V, on a
u(x)  V).
Si
V est un
sous-espace
de
E stable par
u, alors la restriction
de
u à
V est un
endomorphisme
de
V.
V).
Si
V est un
sous-espace
de
E stable par
u, alors la restriction
de
u à
V est un
endomorphisme
de
V.
 ou
ou
 ) muni d'une
base
. On note
(x1, x2, x3, x4) les coordonnées d'un
vecteur dans cette
base
. Soit
ut
) muni d'une
base
. On note
(x1, x2, x3, x4) les coordonnées d'un
vecteur dans cette
base
. Soit
ut  EndK(E) (
t
EndK(E) (
t  K )
définie par
K )
définie par
Pour quelles valeurs du paramètre a l'hyperplan vectoriel Ha d'équation ax1+x2+x3+x4=0 est-il stable par ut?
Pour ces valeurs de a, décrire matriciellement .
 EndK(E). On suppose que
(on dit que
u et
v commutent), alors
Im(u) et
Ker(u)
sont stables par
v.
EndK(E). On suppose que
(on dit que
u et
v commutent), alors
Im(u) et
Ker(u)
sont stables par
v.
Soient E un K- espace vectoriel , u
 EndK(E). A tout
polynôme
(
) on
associe
l'endomorphisme
où
(
i fois).
EndK(E). A tout
polynôme
(
) on
associe
l'endomorphisme
où
(
i fois).
Pour u
 EndK(E) fixé, l'application
définie par
EndK(E) fixé, l'application
définie par
 u(P)=P(u) est un
morphisme d'algèbres
.
Im(
u(P)=P(u) est un
morphisme d'algèbres
.
Im(  u) est une sous-algèbre
commutative de
EndK(E),
ker(
u) est une sous-algèbre
commutative de
EndK(E),
ker(  u) est un
idéal
de
.
u) est un
idéal
de
.
Soient P, , u
 EndK(E).
On suppose que
(P,Q)=1.
Alors
.
EndK(E).
On suppose que
(P,Q)=1.
Alors
.
Plus généralement, si est un élément de tel que pour on ait (Pi,Pj)=1, alors .
| Passer à la Feuille de Travail 12 |
| ou retourner au Sommaire |
Feuille de Travail 12
6.2 Valeurs propres d'un endomorphisme
 EndK(E). On dit que
EndK(E). On dit que

 K est une valeur propre de
u si
. Autrement dit,
K est une valeur propre de
u si
. Autrement dit,

 K est valeur propre
de
u si et seulement si il existe un vecteur non nul
x
K est valeur propre
de
u si et seulement si il existe un vecteur non nul
x  E tel
que
u(x)=
E tel
que
u(x)=  x.
x.
Un vecteur non nul x
 E tel que
u(x)=
E tel que
u(x)=  x est appelé
vecteur propre pour
x est appelé
vecteur propre pour
 .
.
Le sous-espace est appelé sous-espace propre associé à la valeur propre
 .
.
 est
stable par
u et la restriction de
u à
est une
homothétie de rapport
est
stable par
u et la restriction de
u à
est une
homothétie de rapport
 .
.
 EndK(E). On appelle
spectre de
u, noté
spec(u) (ou
sp(u)), l'ensemble des valeurs
propres de
u.
EndK(E). On appelle
spectre de
u, noté
spec(u) (ou
sp(u)), l'ensemble des valeurs
propres de
u.
 EndK(E) définie par
u(P)= P + XP'. Quelles
sont les valeurs propres de
u?
EndK(E) définie par
u(P)= P + XP'. Quelles
sont les valeurs propres de
u?
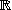 et pour
K=
et pour
K= 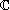 , donner un exemple de
K-
espace vectoriel
E et
u
, donner un exemple de
K-
espace vectoriel
E et
u  EndK(E) tels que
.
EndK(E) tels que
.
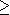 2,
u, v
2,
u, v  EndK(E). Montrer que
et
ont mêmes
valeurs propres.
EndK(E). Montrer que
et
ont mêmes
valeurs propres.
u
 EndK(E),
.
EndK(E),
.
Montrer que si

 spec(u),
alors on a
P(
spec(u),
alors on a
P(  )
)  spec(P(u)).
spec(P(u)).
| Passer à la Feuille de Travail 13 |
| ou retourner au Sommaire |
Feuille de Travail 13
6.3 Réduction d'un endomorphisme en dimension finie
Soient E un K- espace vectoriel de dimension finie n, u un endomorphisme de E. On supposera au besoin E muni d'une base de sorte que u est identifié à sa matrice dans la base .
 EndK(E). Alors
est une valeur propre de
u
si et seulement si
EndK(E). Alors
est une valeur propre de
u
si et seulement si
Si on note In la matrice identité d'ordre n, on a est une valeur propre de u (ou de manière équivalente de M) si et seulement si
 EndK(E) on pose
EndK(E) on pose
On montre que Pu(X) est un polynôme de degré n.
Pu(X) est appelé le polynôme caractéristique de l'endomorphisme u
(ou de manière équivalente, le polynôme caractéristique
de la matrice ).
 Mn(K) une matrice carrée d'ordre
n. On a
Mn(K) une matrice carrée d'ordre
n. On a
- Si un polynôme non nul
admet
 pour
racine de multiplicité
pour
racine de multiplicité
 , alors il existe
tel
que
et
.
, alors il existe
tel
que
et
.
- Si un polynôme non nul
admet
pour racines de multiplicités respectives
, alors il existe
tel
que
et
pour
1
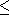 i
i 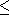 s.
s.
On a .
Si alors Q est une constante non nulle et ( k K). On dit alors que le
polynôme
P est scindé sur
K.
K). On dit alors que le
polynôme
P est scindé sur
K.
- Un corps K sur lequel tout polynôme est scindé est dit algébriquement clos.
Soit
Calculer le polynôme caractéristique PM(X) de M et dire pour quelles valeurs du paramètre PM(X) a une racine double.
 est une racine de multiplicité
est une racine de multiplicité
 du polynôme caractéristique
Pu(X) de
u, alors on a
du polynôme caractéristique
Pu(X) de
u, alors on a
| Passer à la Feuille de Travail 14 |
| ou retourner au Sommaire |
Feuille de Travail 14
6.3 Réduction d'un endomorphisme en dimension finie
 Mn(K) est diagonalisable s'il existe
une matrice inversible
P
Mn(K) est diagonalisable s'il existe
une matrice inversible
P  Mn(K) telle que
est une matrice diagonale.
Mn(K) telle que
est une matrice diagonale.
 EndK(E). Alors
u est diagonalisable si et seulement si il
existe
polynôme non nul à racines simples tel que
P(u)=0.
EndK(E). Alors
u est diagonalisable si et seulement si il
existe
polynôme non nul à racines simples tel que
P(u)=0.
Soit E un K- espace vectoriel de dimension finie n et u
 EndK(E).
EndK(E).
Les assertions suivantes sont équivalentes
- i)
- u est diagonalisable
- ii)
- Le polynôme caractéristique
Pu(X) de
u est
scindé sur
K et pour
toute racine de multiplicité
de multiplicité
 de
Pu(X) on a
de
Pu(X) on a
 EndK(E). Si
u admet
n valeurs propres distinctes
, alors
u est diagonalisable et
chaque
sous-espace
propre
est de
dimension
1.
EndK(E). Si
u admet
n valeurs propres distinctes
, alors
u est diagonalisable et
chaque
sous-espace
propre
est de
dimension
1.
Donner des conditions nécessaires et suffisantes sur les nombres complexes a, b, c pour que la matrice symétrique
- Montrer que est un endomorphisme de EndK(E).
- Montrer que est diagonalisable si et seulement si u est diagonalisable.
une base de E. Soient .
On considère l'endomorphisme u de E défini par
- Calculer le polynôme caractéristique de u pour n=2, n=3 et n=4.
- Trouver une matrice
A
 M4(
M4( 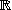 )
n'ayant aucune valeur propre réelle.
)
n'ayant aucune valeur propre réelle.
- Calculer le polynôme caractéristique de u pour n quelconque.
- Montrer que u est diagonalisable si et seulement si u admet n valeurs propres distinctes.
 E tel que
est une
base
de
E. Donner la
matrice de
f dans la
base
.
E tel que
est une
base
de
E. Donner la
matrice de
f dans la
base
.
| Passer à la Feuille de Travail 15 |
| ou retourner au Sommaire |
Feuille de Travail 15
6.3 Réduction d'un endomorphisme en dimension finie
 Mn(K) est trigonalisable s'il existe
une matrice inversible
P
Mn(K) est trigonalisable s'il existe
une matrice inversible
P  Mn(K) telle que
est une matrice triangulaire supérieure.
Mn(K) telle que
est une matrice triangulaire supérieure.
Soit E un K- espace vectoriel de dimension finie n et u
 EndK(E).
EndK(E).
Les assertions suivantes sont équivalentes
- i)
- u est trigonalisable
- ii)
- Le polynôme caractéristique Pu(X) de u est scindé sur K.
Le corps
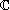 étant algébriquement clos, tout
endomorphisme
u d'un
étant algébriquement clos, tout
endomorphisme
u d'un
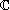 -espace vectoriel de
dimension finie
E est
trigonalisable.
-espace vectoriel de
dimension finie
E est
trigonalisable.
Soit E un K- espace vectoriel de dimension finie n, u un endomorphisme de E. Alors le polynôme caractéristique de u annule u:
Si u a pour matrice M relativement à une base de E, le théorème de Cayley-Hamilton s'énonce
 est une valeur propre de multiplicité
est une valeur propre de multiplicité
 de
u, on appelle sous-espace caractéristique
associé à la
valeur propre
de
u, on appelle sous-espace caractéristique
associé à la
valeur propre
 , le
sous-espace
, le
sous-espace
- Si
 est une valeur propre de multiplicité
est une valeur propre de multiplicité
 de
u, alors le sous-espace caractéristique
est de
dimension
de
u, alors le sous-espace caractéristique
est de
dimension
 .
.
- Si le polynôme caractéristique de est scindé sur K, alors E est somme directe des sous-espaces caractéristiques associés aux valeurs propres de u.
Alors pour tout i ( 1
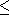 i
i 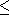 s) il existe une
base
s) il existe une
base
telle que
est une base de E dans laquelle la matrice de u est triangulaire supérieure.
 Mn(K) une matrice
dont le polynôme caractéristique est
scindé sur
K:
Mn(K) une matrice
dont le polynôme caractéristique est
scindé sur
K:
Alors il existe une matrice inversible P
 Mn(K) telle que
Mn(K) telle que
La matrice M' ci-dessus est dite diagonale par blocs.
tel que le polynôme caractéristique de u soit scindé sur K.
Alors u s'écrit d'une manière et d'une seule sous la forme
où d est un endomorphisme diagonalisable,
n un endomorphisme nilpotent
et dn=nd ( n et d commutent).
| Retourner à la Feuille de Travail 14 |
| ou aller au Sommaire |
Sessions Wims
Exercice ia1Corps
Un corps est un anneau commutatif dont l'ensemble des éléments non nuls est un groupe multiplicatif.- où p est un nombre premier
-
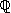 , corps des nombres rationnels
, corps des nombres rationnels
-
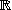 , corps des nombres réels
, corps des nombres réels
-
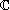 , corps des nombres complexes
, corps des nombres complexes
- si K est un corps, un polynôme irréductible, est un corps.