Special relativity and steps towards general relativity
--- Introduction ---
This module contains 9 elementary exercises that can be
used as part of a semester-length "special
relativity and steps towards general relativity" (SR +
εGR) Wikiversity course.
You should first study the pdf presentations, or find equivalent
material elsewhere, e.g. the reading list at the above URL. The pdf
slides can be presented by teachers as fullscreen lectures in a
classroom, or by students as personal study guides on a desktop
computer. They have clickable links to Wikipedia articles that add
considerable depth to key ideas. You may use the Wikiversity page to
find other people (with a fuzzy line between students and teachers) to
discuss or improve any aspect of the course, including your own
progress in learning, using the open, collaborative wiki culture. These WIMS
exercises are published under the GPL licence, allowing you to improve
and redistribute them (under the conditions of the GPL), or install them on a
local WIMS server in a "class" in which students' scores are recorded
and used for formal tutorial or examination grades.
You should select exercises corresponding to the material that
you feel you already understand. The numerical order approximately
corresponds to the pedagogical sequence.
In version 1.00 of this module, it is the student's responsibility
to carry out the key element of SR exercises, since WIMS will not force
you to do this: draw a correct spacetime diagram for
the problem and show yourself what "simultaneous" means to different
observers. Pen and paper still constitute a powerful
computational tool set.
The "printable version" button below may give several errors if you are
using this exercise on an old (3.62 or older) version of WIMS and/or version
1.00 of this module.
1.1.1 GR - tensors and 1-forms, numerica
At the point x in a 4D pseudo-manifold M, there is a tensor that can be written in the coordinate basis {
} as . The metric g written in the same coordinate basis and evaluated at the same point x is . Hint: this is written in octave format as
.
1.1.2 GR - tensor type, order, dimension
Tensors over a -dimensional pseudo-manifold M can be expressed using a coordinate basis that has a vector basis {
}. Let us What are
,
, and other properties of the following tensors?
0.1.3 SR - 2D Minkowski diagram
1. Is a valid matrix on
2D space? The corresponding may be different from above.
2. What is of the rocket with respect to the Sun?
3. What is the matrix Λ for the coordinates of an event in the rocket's (x',t') space, i.e. where ? The components of the matrix are written .
0.1.4 SR - 2D Minkowski diagram
A rocket passes the Sun travelling at constant speed towards a planet at AU from the Sun. The planet is considered to be at rest for this calculation. When the rocket passes the Sun, a clock on the rocket is set to agree with a clock on the Sun, which happens to read 0 s. The Sun and the planet have clocks that were previously synchronised. An observer at the Sun continually sends photons along the rocket's path in order to synchronise spacetime events; the photons bounce off a mirror on the rocket.
Draw a diagram.
1. What does the rocket clock read when the rocket passes the planet?
2. When the planet's clock reads the number of seconds in the answer to question 1, where does the observer at the Sun think the rocket is?
3. A flare occurs on the Sun s after the rocket passed. For the rocket at the time it passes the planet, does the flare occur in the past, present (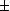 0.1 s) or future?
0.1 s) or future?
0.1.2 SR - simultaneity is not absolute
We continually send photons towards a of rest-frame length ns in order to synchronise spacetime events on the . The photons bounce off mirrors at the front and back of the . The is us . At the moment that the of the passes by us (very close to us), the front and back headlights of the flash on for just a moment, simultaneously in the 's spacetime frame.
Draw a diagram.
1. In our spacetime frame, does the flash at the of the happen before, simultaneously to, or after the flash when the of the is passing us?
2. When does the flash at the of the happen in our reference frame (the of the passes us at
s)?
3. How far from us does the flash at the of the happen in our reference frame (the of the passes us at
s)?
4. How long is the in our reference frame?
0.2.1 SR - 4-velocity vs Newtonian speed
An AGN blob is moving away from us radially (label this the
axis) at constant speed β, with 4-velocity
. Write the following expressions using β,
, and/or φ, where β=tanh φ. The sign convention is .
0.2.2 SR - invariance and conservation
,
.
0.2.3 SR - mass, energy, momentum
Two s, each of rest-frame length ns and (rest) mass kg travel towards each other at identical . They smash into each other, and thanks to modern technology nobody gets hurt. They remain stuck together as a single post-crash , which is not moving. The system is self-contained and no form of energy is emitted or transmitted outside of the system (e.g. Planck radiation is negligible, no heat is transferred to the surroundings, etc.; also, no energy enters the system).
Syntax: Avoid using "+" in the exponent of large numbers, e.g. write 3e8, not 3e+8. Small numbers must be written without an exponent, e.g. write 0.0314, not 3.14e-2.
0.1.1 SR - definitions
Match!
This page is not in its usual appearance because WIMS is unable to recognize your
web browser.
Please take note that WIMS pages are interactively generated; they are not ordinary
HTML files. They must be used interactively ONLINE. It is useless
for you to gather them through a robot program.
- Description: elementary relativity exercises. ((c) GPL and/or CC-BY-SA-3.0 or later). This is the main site of WIMS (WWW Interactive Multipurpose Server): interactive exercises, online calculators and plotters, mathematical recreation and games
- Keywords: wims, mathematics, mathematical, math, maths, interactive mathematics, interactive math, interactive maths, mathematic, online, calculator, graphing, exercise, exercice, puzzle, calculus, K-12, algebra, mathématique, interactive, interactive mathematics, interactive mathematical, interactive math, interactive maths, mathematical education, enseignement mathématique, mathematics teaching, teaching mathematics, algebra, geometry, calculus, function, curve, surface, graphing, virtual class, virtual classes, virtual classroom, virtual classrooms, interactive documents, interactive document, physics, Minkowski diagram, special relativity, general relativity, tensor field
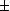 0.1 s) or future?
0.1 s) or future?