Nombres complexes (équations)
Sommaire
Ce cours traite des nombres complexes dans le contexte des équations. Il recouvre et déborde, parfois de façon importante, le programme des mathématiques expertes des terminales déjà abordé dans le cours WIMS Nombres complexes (trigonométrie et géométrie) .
Pour vous assurer de vos connaissances de base sur les nombres complexes, consultez le cours WIMS Nombres complexes (introduction) et testez-vous sur les exercices. Le cours WIMS Géométrie du plan complexe décrit les isométries et les similitudes du plan complexe avec exercices et figures.
Nous commençons par un panorama des liens entre Ensembles de nombres et équations .
Mathématiques expertes
Equations du second degré
- Racines carrées d'un nombre complexe
- Équations du second degré à coefficients réels
- Équations du second degré dans C
- Exercices sur les racines d'un trinôme de degré 2
Autres équations
- Polynômes
- Factorisation d'un polynôme
- Factorisation des polynômes à coefficients réels
- Factorisation dans C[X]
- Exercices sur factorisation et équations polynomiales
- Équations en z et en conjugué de z
Racines n-ièmes d'un nombre complexe
- Racines n-ièmes de l'unité
- Racines cubiques d'un nombre complexe
- Racines n-ièmes d'un nombre complexe
- Racines n-ièmes de l'unité et polygones
- Construction du pentagone régulier
Pour aller plus loin...
Ces chapitres supposent une certaine pratique du calcul ou permettent de l'acquérir !- Relations entre coefficients et racines
- Formules de Viète
- Exercices d'applications des formules de Viète
- Résolution par radicaux d'une équation de degré 3
- Transformation de Fourier discrète (TFD)
- TFD : Définition, exemples, exercices
- Ensemble de Mandelbrot, quelques résultats.
Ensembles de nombres et équations
Les divers ensembles de nombres que vous connaissez sont reliés à la recherche de solutions d'une équation. Cet exposé privilégie cette approche ; il n'est pas historique mais ce tour d'horizon est instructif.
Ensemble
Au début étaient les nombres entiers naturels, désignés par des symboles appelés chiffres : 1, 2, 3..., auxquels on adjoignit ultérieurement le zéro. À ces nombres furent associées des opérations : addition et multiplication de deux entiers naturels. On obtint l’ensemble et on sait dès lors ce que signifie le nombre 4865, en écriture décimale.
Dans cet ensemble, l’équation a une solution : . Mais l'équation n'a pas de solution dans . Cette équation a une solution dans un ensemble qui contient .
Ensemble
Cet ensemble, nommé , est l'ensemble des entiers relatifs. Il contient et d'autres nombres : les solutions des équations qui se ramènent au type avec et . Ces nouveaux nombres sont les opposés des entiers naturels, on les note . L'équation a maintenant une solution dans : .
Dans , sont définies une addition et une multiplication qui prolongent celles de .
Dans , l'équation n'a pas de solution ...
Ensemble
L'ensemble des nombres rationnels contient et d'autres nombres, les solutions des équations qui se ramènent au type (où , non nul, n'est pas un multiple de ). On écrit ces nombres comme des fractions : où et sont des entiers relatifs, avec . Cette écriture est précisée par des règles d'égalité : si et seulement si .
On définit aussi des opérations, addition et multiplication dans qui prolongent celles de . Dans cet ensemble tout élément a un opposé et tout élément non nul a un inverse. En résumé, les quatre "opérations" sont possibles : addition, soustraction, multiplication et division, on dit alors que est un corps.
On démontre assez facilement que les nombres rationnels ont un développement décimal soit fini, soit périodique à partir d'un certain rang. C'est une propriété caractéristique de ... Exemples : 1,235 ou -15,235785678567856... avec une répétition infinie du bloc 7856.
L'équation n'a pas de solution rationnelle. Si est un nombre positif vérifiant cette équation, nous démontrons ici qu'il n'est pas rationnel.
Ensemble
L'ensemble des nombres réels contient et d'autres nombres dits irrationnels. Parmi les nombres irrationnels, on trouve évidemment , , ... Il en existe d'autres comme par exemple, le rapport constant entre la circonférence d'un cercle et son diamètre qui est noté et dont une valeur approchée est Le développement décimal de ce nombre n'est pas périodique. Un autre exemple est le nombre : c'est le nombre réel dont le logarithme népérien vaut . Une valeur approchée est
Dans , on définit aussi une addition et une multiplication qui prolongent celles de .
Mais dans , l’équation n'a pas de solution.
Ensemble
Nous finissons notre tour d'horizon des ensembles par l'ensemble des nombres complexes. Historiquement, l’idée des nombres complexes est apparue pour aider à la résolution des équations de degré trois (voir cette page ). On a défini un nombre noté qui, par définition, est une solution de l’équation et vérifie donc l'égalité .
Avec et les nombres réels, grâce aux opérations prolongeant celles de , on construit de nouveaux nombres ( ) qui forment l'ensemble .
Cet ensemble a de nombreuses propriétés algébriques et géométriques vues dans ce cours et les précédents.
Racines carrées d'un nombre complexe
Soit un nombre complexe non nul. On cherche les nombres complexes vérifiant .
À ces deux égalités, on adjoint souvent une troisième, qui facilite la résolution. Elle porte sur l'égalité des modules de et : .
On obtient les trois égalités :
Des première et troisième équations, on déduit une solution pour (par exemple), puis, en prenant les racines carrées, deux valeurs pour : et . En reportant ces valeurs de trouvées dans la seconde équation , on obtient les valeurs correspondantes pour : et . L'ensemble des solutions cherchées de est donc :
.
Pour achever la démonstration, on vérifie que la troisième égalité est bien satisfaite, ce qui est le cas.On obtient donc deux solutions : et . Comme vaut , on a bien deux solutions opposées.
On en déduit , donc et les valeurs correspondantes pour : . Les deux racines de sont et .
2. Avec l'écriture exponentielle, calculer les racines de . On peut écrire : . En appliquant ce qui a été dit plus haut, on obtient : et .
Dans les exercices, on choisira la méthode adaptée à la forme des données.
Calculer avec l'écriture algébrique, puis avec l'écriture trigonométrique, les racines carrées de . En déduire les valeurs de et de .
- Si l'on note , alors on peut écrire :
On en déduit facilement les deux racines carrées :
et
On obtient ainsi les deux racines carrées. et- Par , on sait que les sinus et cosinus de sont positifs.
Par , on sait que les sinus et cosinus de sont négatifs.
On trouve donc : et
Exemple à données aléatoires
- On écrit ce que signifie l'équation
en termes de
et de
.
Comme , l'équation est équivalente au système d'équationsOn peut a priori résoudre à partir de ces deux équations. Mais on va en utiliser une autre qui va simplifier la résolution
- On traduit donc le fait que
ce qui donne
-
Et quand on a la valeur de
et celle de
, que
voulez-vous faire d'autre que d'en déduire la valeur de
et de
en ajoutant et retranchant ces deux équations ?
Au fait, voyez-vous une raison a priori pour que ces valeurs soient positives ?
- Quelle condition n'a-t-on pas utilisée ?
. Ainsi
et
sont de même signe. On a donc
et
avec une contrainte sur les signes
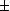 .
.
et en approchant et .
Équations du second degré à coefficients réels
Il s'agit d'un cas particulier important de l'étude générale qui sera reprise à la page suivante.
Avant de résoudre une équation du second degré dans , révisez la résolution de l'équation du second degré à coefficients réels dans le cours Trinôme du second degré , et en particulier la mise sous forme canonique. La résolution des équations du second degré dans suit exactement la même démarche, ce qui conduit à calculer la racine carrée du discriminant et, dans , c'est toujours possible.
Si
sont réels, alors
est un réel positif ou négatif.
1. Si
est positif ou nul, on est ramené à l'équation du second degré connue, dont on connaît les solutions.
2. Si
est négatif, puisque l'on résout maintenant dans
, on peut poser
avec
,
et les deux racines de
, c'est-à-dire les nombres dont le carré vaut
, sont
.
L’équation, dans ce cas particulier où les coefficients sont réels, admet ainsi deux racines complexes conjuguées :
et
Leurs images dans le plan complexe sont symétriques par rapport à l'axe réel.Le discriminant vaut Les solutions de l'équation sont donc : . L’ensemble des solutions est donc . Elles sont représentées dans le dessin ci-dessous.

Équations du second degré dans C
Dans le prolongement de la page précédente, nous traitons ici de la résolution des équations du second degré à coefficients complexes. La résolution dans suit exactement la même démarche, ce qui conduit à calculer une racine carrée du discriminant qui peut être un nombre complexe quelconque et, là encore, c'est toujours possible.
1. Résoudre dans l' équation .
Comme 0 n'est pas solution de l’équation, on divise les deux membres de l'équation par , et on regroupe judicieusement...
On arrive à l'équation : (*) . On calcule .
On obtient deux solutions de l'équation (*), et . il ne reste plus qu'à résoudre les deux dernières équations et
2. Résoudre dans l'équation où est un nombre complexe donné non nul. Montrer que les racines de cette équation sont les affixes des sommets d'un triangle rectangle isocèle.
Exemple à données aléatoires.
Le discriminant est
.
On calcule les racines carrées de
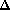 par la
méthode algébrique
:
ou
.
Les racines de l'équation sont alors
et
par la
méthode algébrique
:
ou
.
Les racines de l'équation sont alors
et
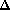 est nul.
est nul.Exercices sur les racines d'un trinôme de degré 2
Le résultat suivant, déjà énoncé dans le cas de la résolution dans (voir cette page ), peut être utile dans certains cas et souvent pour une vérification des solutions.
et .
- Racines d'un polynôme quadratique.
- Exercices sur les racines doubles.
- Lien entre racines et coefficients.
-
Que peut-on dire de la différence des racines ?
Solution. On se place dans le cas où p est imaginaire pur, et q réel. L'autre cas de l'exercice (il y en a deux) se traite de façon analogue.
Soit et . L'hypothèse voulant que z1 et z2 ne soient ni réels ni imaginaires purs, cela revient à dire qu'aucun des termes a1, a2, b1, b2 n'est nul. 1- La somme des racines vaut -p. Donc .
Puisque -p est imaginaire pur, a1 + a2=0.
D'où : et 2- Le produit des racines vaut q. Donc . Il est réel donc b2- b1=0 Et et .
Donc z1 - z2 = 2a1 est réel.
Polynômes
- Soient des nombres réels ou complexes (les coefficients) avec , et z une variable réelle ou complexe. Un polynôme P est une somme algébrique finie de la forme : .
- Le degré d'un polynôme non nul est l'entier naturel n.
-
Une fonction polynôme est une fonction
f de
dans
, qui à
.
- On appelle racine d'un polynôme, toute valeur z qui annule la fonction polynôme f, toute solution de l'équation f(z)=0.
- L'ensemble des polynômes à coefficients réels est noté , le sous-ensemble-ensemble des polynômes de degré n est noté , l'ensemble des polynômes à coefficients complexes est noté .
Remarque. Dans la pratique, on notera un polynôme soit par une lettre majuscule P, soit sous la forme P(z) ou P(x) pour indiquer le nom de la variable, sans pour autant le confondre avec la fonction polynôme.
Soit P un polynôme de . Si z0 est une racine de P, alors est une autre racine de P.
. En utilisant les propriétés des conjugués et le fait que tous les coefficients ai sont réels, c'est-à-dire pour tous les indices, On en déduit . Donc qui annule P est aussi une racine de P.
On rappelle une identité remarquable très utile dans ce chapitre (vérifiez-la !) :
Solution
z5+32 = (z+2)( z4 -2z3 +4z2 -8z +16)
Factorisation d'un polynôme
Il existe donc un polynôme vérifiant (*)
Démonstration.
Sachant que
P(a) = 0, on peut écrire :
.
Dans toutes les expressions
(zk-ak),
, on peut mettre en facteur
(z-a) grâce à l'
identité remarquable
vue précédemment.
D'où le résultat.
Remarques.
- Ce théorème est en fait une équivalence.
- En général, on trouvera Q en développant les deux membres de l'égalité (*), et en identifiant les termes de même degré. Voir pages suivantes.
- Si P est un polynôme de , Q est aussi un polynôme de . Ceci découle facilement de la démonstration ci-dessus.
Soit P= (z-a) Q. Si Q s'annule pour la valeur a, on dit que a est une racine double (au moins) de P et il existe tel que Q=(z-a) S, et P s'écrit : P= (z-a)2 S.
S'il existe un entier naturel p, non nul, et un polynôme P1 de tel que P= (z-a)p P1 avec , on dit que P admet a pour racine d'ordre p et que p est l'ordre de multiplicité de la racine a.
Factorisation des polynômes à coefficients réels
Factorisation d'un polynôme de degré 2.
Soit P2 un polynôme de degré 2 de (à coefficients réels) : P2= a2 z2+ a1 z + a0 avec . On a vu ici que P2 a deux racines z1 et z2, éventuellement confondues, dans .- Si les deux racines sont réelles, P2 se factorise dans en un produit de deux polynômes de degré 1 : P2=a2(z-z1)(z-z2).
- Si les deux racines ne sont pas réelles, comme on l'a vu ici , elles sont conjuguées et P2 se factorise en un produit de deux polynômes de degré 1 :
Factorisation d'un polynôme de degré 3.
Soit P3 un polynôme de degré 3 à coefficients réels : P3 = a3 z3 + a2 z2 +a1 z +a0 avec .Soit
P3 un polynôme de degré 3 à coefficients réels. D'après la propriété,
on peut trouver, d'une façon ou d'une autre, une racine réelle
de
P3 pour le factoriser. En effet,
d’après le théorème de factorisation (voir
ici
), il existe
tels que
P se factorise sous la forme :
. Posons
Q = a3 x2 + a4 x +a5
On détermine
Q en développant les deux membres, puis en identifiant les
termes de même degré, en vertu de l'unicité de l'écriture d'un polynôme.
Il ne reste plus qu'à factoriser ce polynôme de degré 2 comme on l'a fait plus haut.
Ceci est équivalent à a=1, b =0 et c = -4 et on obtient P(x)= (x-1)(x2-4) =(x-1)(x-2)(x+2).
A. Factoriser les polynômes suivants dans (on commencera pas trouver, en faisant des essais, une racine réelle simple...).
- P1(x) = x3-4x2 -7x +10.
- P2(x)=6x3+11x2-3x-2.
- P3(x)=x3-x2-x-2.
- P1(x) = x3-4x2 -7x +10 =(x-5)(x-1)(x+2).
- P2(x)=6x3+11x2-3x-2 = (x+2)(2x-1)(3x+1).
- P3(x)=x3-x2-x-2 = (x-2)(x2+x+1).
B. Factorisation
Factorisation dans C[X]
Jean Le Rond d'Alembert est le premier à avoir énoncé, sous une forme complète, le théorème fondamental de l'algèbre, souvent nommé simplement de d'Alembert, déjà avancé par Viète et Girard mais qui n'arrivèrent pas à le démontrer de façon précise. (Tiré de ChronoMath )
Le théorème de d'Alembert permet de dire que, si Pn est un polynôme non constant de degré n, il existe un nombre complexe z1 racine de Pn et un polynome de degré n-1, tels que . On applique à répétition le théorème de d’Alembert (démonstration par récurrence) :
le polynôme est de degré 1 et de la forme , avec a,b complexes, a non nul.
On met en valeur la racine de P1 : , d'où
.
On a ainsi mis en évidence les n racines du polynôme , distinctes ou confondues.,
Exercices sur factorisation et équations polynomiales
1. Sachant que est racine du polynôme P(X) = X4-2X3+6X2+22X+13, factoriser ce polynôme dans .
Il existe donc un polynôme Q tel que . Q est un polynôme de degré 2, que l'on détermine facilement en développant les deux membres, comme dans l'exemple ci-dessus, et en identifiant les termes de même degré. On trouve Q = X2+2X+1 =(X+1)2. La factorisation de P dans est : P=(X2-4X+13)(X+1)2
2. Trouver toutes les solutions dans de l'équation E : , sachant qu'elle admet une solution réelle.
Solution. Soit x cette solution réelle. Si elle est solution, alors (implication) la partie imaginaire de est nulle, c'est-à-dire x vérifie 2x2-5x+2=0, équation qui admet deux solutions et x = 2.
Il reste à regarder quelles valeurs satisfont l'équation donnée (on a raisonné par implication). Seule x=2 convient et on peut, dès lors, factoriser par (z-2).
En identifiant les termes de même degré, on arrive à b2 =1, b1= -1+2i, b0= -3-i. L'équation E devient : . L'équation de degré deux admet pour solutions : et .
Les solutions de E sont : 2, et .
3. Factoriser le polynôme :
4. On cherchera une racine imaginaire pure des polynômes suivants, puis on les factorisera :
.
Solution.
.
- La solution imaginaire pure est .
- Le polynôme se factorise en . Les racines du polynôme de degré deux sont et
.
5. Résoudre dans l'équation z4 - 6z3 + 14z2 -24z + 40 = 0 sachant qu'elle admet deux solutions imaginaires pures.
Avec un peu de travail on arrive à la factorisation par ci-dessous :
z4 - 6z3 + 14z2 -24z + 40 = (z2+4)(z2-6z+10).
Les 4 solutions sont , , et .
Soit le polynôme :
- Trouver une racine z2 de P(z) de la forme , où a est un réel à déterminer. En déduire une factorisation de P en un produit d'un polynôme de degré un et d'un polynôme de degré deux, dont on cherchera les racines. Mettre les trois racines sous forme exponentielle.
- Montrer que les deux suites z1,z2,z3 et z3,z2,z1 sont des suites géométriques dont on donnera la raison.
- Les racines sont , et . Les formes exponentielles sont :
- La première suite a pour raison , la seconde .
Soit P= x7 +x6 +x5 +x4 +x3 +x2 +x + 1
- Factoriser P dans .
- Factoriser P dans .
P est la somme de 8 termes de la suite géométrique de premier terme 1 et de raison x. Puisque 1 n'est visiblement pas solution de l'équation, on peut écrire : .
Les racines de P vérifient : .
On en déduit la factorisation de P dans :
À partir de celle-ci, on obtient la factorisation dans en regroupant deux par deux les racines conjuguées (voir Exercice 2 ci-dessus) :
Équations en z et en conjugué de z
. D'où le résultat.
Écrivons le problème avec la forme algébrique :
On écrit l'égalité des parties réelles et imaginaires : La dernière égalité 4a3 b - 4a b3=4a b ( a +b)(a -b)=0 fournit 4 possibilités pour les valeurs de a que l'on reporte dans la première égalité pour avoir les valeurs de b correspondantes :
1. a=0 qui conduit à b=0
2. b=0 qui conduit à
3. a=b qui conduit à
4. a= -b qui conduit à
L'ensemble des solutions est : .
- Si n=0, on résout , soit et donc . Les solutions sont les affixes des points du cercle de centre O et de rayon 1.
- Si n=1, on résout . Une seule solution z=1.
- Si n=2, on résout . Tous les réels sont solutions.
- Si , on résout . Cette égalité implique (nécessité d'une réciproque) : . Ce qui conduit à : .
Donc :
1. soit .
2. soit qui est équivalent à .
Dans ce dernier cas, on a simultanément les deux égalités et , ce qui implique zn = 1. On obtient ainsi les n racines n-ièmes de l'unité. Sont-elles toutes solutions ?
Réciproquement : Soit une racine quelconque de l'unité, avec .
1.
2.
Toutes les n racines n-ièmes de l'unité conviennent donc.
Conclusion : Si , les solutions sont z=0 et les racines n-ièmes de l'unité.
- Solution de la première équation :
- Solution de la deuxième équation :
Racines n-ièmes de l'unité
L'équation zn=1 admet, dans , n solutions distinctes qui s'écrivent :
où k est un entier prenant n valeurs consécutives, par exemple
On note l'ensemble des racines n-ièmes de l'unité. . On peut donc factoriser le polynôme zn-1 dans :
La somme des n racines n-ièmes de l'unité, pour , est nulle.
. On note , donc

I. Démontrer les résultats suivants : .
- Écrivons alors le nombre complexe z sous la forme exponentielle, , avec réel quelconque. L'équation s'écrit alors :
- Égalité des modules. donc (déja vu) ou
- si on peut écrire : . Les solutions sont les racines sixième de l'unité, et on a raisonné par équivalence.
- Conclusion. L'équation a 7 solutions distinctes : z=0 et , avec .

I. Dans , on a vu que vaut . Montrer l'égalité , puis
II. Soit
, avec
, l'une quelconque des
n-1
racines n-ièmes de l'unité (différente de 1, puisque
p est supposé non nul).
Montrer l'égalité :
Solution. Il s'agit de calculer la somme de n termes d'une suite géométrique de premier terme 1 et de raison . Donc Comme , cela démontre le résultat. On retrouvera ce résultat grâce aux formules de Viète.
- Sur les racines cubiques de l'unité
- Sur les racines cinquièmes de l'unité
- Sur la somme des racines de l'unité (on pourra utiliser l'identité remarquable vue à cette page .)
Racines cubiques d'un nombre complexe
Démonstration.
Si l'on écrit u sous forme exponentielle ( r>0) , on cherche ( ) vérifiant z3=u, c'est-à-dire . Cette condition nécessaire et suffisante s'écrit en système de cette façon :
La résolution du système donne : et (avec ), on obtient donc trois racines cubiques distinctes :
Remarque géométrique.
Si, dans le plan complexe, on considère les trois points M1, M2 ,M3 d'affixes respectives z1, z2 ,z3, puisqu'elles ont le même module, les trois points sont sur le cercle de centre O et de rayon .
Les angles sont égaux, et égaux à . Le triangle M1 M2 M3 est donc un triangle équilatéral (voir Racines n-ièmes de l'unité et polygones ).
Ci-dessous un exemple avec et ses racines cubiques.

Racines n-ièmes d'un nombre complexe
l'entier
k prenant les
n valeurs consécutives comprises entre
0 et
n-1.
1. Calculer les racines cinquièmes de .
2. Calculer les racines quatrièmes de .
- Quel est le degré du polynôme
- Soit , Résoudre l'équation P(z)= 0, et compter le nombre de solutions.
Le polynôme P(z) est de degré 2n -1 ce que l'on vérifie facilement avec la formule du binôme de Newton.
L'identité permet la factorisation :
- Pour n =1, l'équation a une seule solution : . Cette solution reste d’ailleurs valable pour tout , du fait de la factorisation indiquée dans l'aide. Notons de plus que est une racine de multiplicité d'ordre n de P.
- Supposons et cherchons les solutions autres que . Comme le degré de P est 2n-1, il en reste n-1 à trouver : .
Pour , l'équation est équivalente à soit . Pour chacune des solutions, par exemple zk, le nombre est donc une racine n-ième de l'unité . On a vu que les racines n-ième de l'unité sont avec . Ici k est différent de 0 car ne vaut jamais 1. L'égalité est donc équivalente à ( découle de ).
Par la méthode vue au chapitre "Somme d'exponentielles complexes" (dans le cours "Nombres complexes (trigonométrie et géométrie)"), on arrive à : pour . On vérifiera que le dénominateur est toujours non nul.
Conclusion : Pour , on obtient - est, on l'a vu, une racine d'ordre n, on a obtenu ci-dessus n-1 racines supplémentaires, on a bien les 2n-1 (le degré du polynôme) racines distinctes ou confondues annoncées par le théorème de d'Alembert.
- Résoudre dans l'équation z4+1=0, puis factoriser le polynôme P= z4+1 dans
- Vérifier que . Représenter les racines de P dans le plan complexe.
- En déduire une factorisation dans (avec des coefficients uniquement réels).
Les racines carrées de sont (on le vérifiera) et .
Celles de sont (on le vérifiera) et
On en déduit la factorisation de P dans :
- .
- Dans l'expression de P trouvée à la première question on regroupe les facteurs 1 et 4, puis 2 et 3, et on applique le résultat de la deuxième question.
Racines n-ièmes de l'unité et polygones
Consultez ce cours
DOC Polygones convexes réguliers
pour des rappels sur les polygones convexes réguliers.
On utilise ici la caractérisation suivante :
Un polygone convexe est régulier si ses sommets sont sur un cercle et ses angles au centre égaux.

Pour n = 6,voici les racines n-ièmes de l'unité dans le plan complexe ; avec . vous pouvez changer aléatoirement la valeur de n ou la choisir vous-même (inférieure à 50) dans cette case :
Ensuite,- Regardez les différences entre n pair et impair
- Essayez successivement des valeurs multiples, par exemple 2, 4, 12 ou 3, 6, 12, 24
n = 6
Construction du pentagone régulier
Rappels : Polygones réguliers , construction à la règle et au compas{ 1, , , , }.
-
Montrer que
,
,
et
sont les racines du
polynôme
P(z)= z4+z3+z2+z+1.
Utiliser l'identité : z5 - 1 = (z-1)(z4 + z3 + z2 + z + 1)
- On pose et . Montrer, en calculant leur somme et leur produit (voir Relations entre coefficients et racines ), que A et B sont les racines du polynôme t2 + t - 1. Calculer A et B.
- En déduire les valeurs de et .
- On trace le cercle
de centre
d'affixe
passant par le point
D d'affixe
.
Montrer que
coupe l'axe des réels aux points d'abscisse
et
. On utilisera l'
équation complexe d'un cercle.
On rappelle que le cercle de centre , d'affixe et de rayon r est l'ensemble des points d'affixe , avec
- En déduire une construction du pentagone régulier à la règle et au compas. Faites-la avec le module Règles et compas .
- Les éléments de sont les solutions de l'équation z5-1=0 ; or on a : z5-1=(z-1)(z4+z3+z2+z+1) ; les racines de P(z)=z4+z3+z2+z+1 sont les éléments de différents de 1.
- Le nombre A + B vaut , donc -1 puisque est racine du polynôme P.
De , on tire
Le polynôme du second degré en t dont la somme des racines vaut -1 et le produit des racines vaut aussi -1 est bien : t2 + t - 1. Ses racines valent et .
On note que la première est positive et la seconde négative. Laquelle est A, et laquelle est B ?
qui est positif du fait de la double inégalité On en déduit : et . - Les valeurs des deux cosinus résultent de la question 2 : et
- Le rayon du cercle est . L'équation du cercle est : (). L'intersection de avec l'axe de abscisses est réalisée pour et . Ce sont donc les points d'affixe et
- On commence par tracer le cercle trigonométrique de centre O et le point G de coordonnées (1,0). On trace ensuite le cercle défini dans l'énoncé (en vert sur la figure ci-dessous) qui coupe l'axe des abscisses (on l'a vu) en et .
On trace ensuite la perpendiculaire à (O G) au point d'affixe qui recoupe le cercle trigonométrique en deux points H et K. De , on tire l'égalité (mod ). Les points G et H sont donc les sommets du pentagone, par symétrie K également.
On fait de même au point d'affixe et on obtient les deux derniers sommets I et J. Il ne reste plus qu'à tracer les côtés de G H I J K

Relations entre coefficients et racines
Polynôme du second degré.
Cette page, et celle qui suit, se proposent de généraliser ce résultat vu ici (assorti de techniques de vérification) :
En identifiant les deux dernières écritures, on obtient le résultat annoncé.
Remarque. On a vu dans le premier exercice de Factorisation des polynômes à coefficients réels qu'un polynôme de s'écrit en fonction de ses racines complexes et sous la forme : . On retrouve le fait que le produit vaut et la somme .
Ces relations permettent d'établir l'équation du second degré vérifiée par deux inconnues et d'ainsi les calculer.
- Calculer la somme et le produit des racines sans les calculer.
- Trouver deux nombres connaissant leur somme et leur produit
- Calculer la valeur de résistances
Polynôme du troisième degré.
Le polynôme P3(z) = a3 z3+a2 z2+a1 z+ a0, (*) (avec ) admet dans trois racines distinctes ou confondues z1, z2 et z3. Il se factorise donc sous la forme : P3(z) = a3(z-z1)(z-z2)(z-z3). En développant cette expression (faites le !), on obtient :(**).
En identifiant les deux écritures (*) et (**) du polynôme (unicité de l'écriture), on obtient :
Polynôme du quatrième degré.
- Refaire le même calcul que ci-dessus avec un polynôme de degré 4.
- Comparer les résultats obtenus avec les résultats précédents. En regardant la forme des résultats, que peut-on conjecturer ?
1. Ce polynôme que l'on écrira P4(z) = a4 z4 +a3 z3+a2 z2+a1 z+ a0, (*) (avec ) admet dans quatre racines distinctes ou confondues z1, z2,z3 et z4. Il se factorise donc sous la forme : P4(z) =a4(z-z1)(z-z2)(z-z3)(z-z4). En le développant (faites le !), on obtient :
(z1 z2+z1 z3 + z1 z4 + z2 z3+ z2 z4 +z3 z4) z2 (**).
En identifiant les deux écritures (*) et (**) du polynôme (unicité de l'écriture), on obtient : 2. La forme un peu particulière des résultats est indiquée ci-dessous.Généralisation.
En regardant ces trois résultats, on commence à voir des régularités ... Dans les trois cas, on a pris les produits des racines une par une et on en a fait la somme, puis les produits deux par deux et on en a fait la somme, puis les produits trois par trois et on en a fait la somme... etc.- Le dénominateur est toujours le coefficient du terme de plus haut degré.
- Les indices des numérateurs sont dans un ordre régulier décroissant, et on observe une alternance de signe.
Formules de Viète
Soit P un polynôme de degré n, à coefficients complexes, de la variable z complexe. Il existe donc un (n+1)-uplet de complexes, coefficients de P, , avec tel que : . Ici , on a vu que ce polynôme admet, dans , n racines distinctes ou confondues : . Ces racines sont notées par des noms différents mais peuvent être égales pour certaines d?entre elles (racines doubles, triples...).
On définit maintenant de façon générale les sommes de produits de racines qu'on a vu apparaître à la page précédente .
Soit p un entier naturel, . On appelle polynômes symétriques élémentaires les expressions notées des n variables définies par :
.
Dans le cas où les variables sont les racines d'un polynôme P, le nombre est la somme de tous les produits de p racines de P, choisies parmi les n racines, ces p racines étant choisies de toutes les manières possibles.
- (Somme de tous les produits possibles de une racine, c'est-à-dire somme des racines)
- (Somme de tous les produits possibles de deux racines)
- (Somme de tous les produits possibles de trois racines)
- (Somme de tous les produits possibles de quatre racines, un seul produit)
Les valeurs des poynômes symétriques des racines d'un polynôme s'expriment en fonction des coefficients du polynôme par les formules de Viète.
Exercices d'applications des formules de Viète
- Calculer, sans utiliser les valeurs des racines, , puis .
- En utilisant que l'on exprimera de deux manières différentes, en déduire la valeur de
- a0 = -6, a1 = 7, a2 = -4, a3 = 2
- .
- , puisque , et sont des racines de P. Donc . Calculons-le autrement:
On en déduit :
Polynômes symétriques
- Longueur de deux côtés de l'angle droit d'un triangle rectangle dont on connaît le périmètre
- Longueur de deux côtés de l'angle droit d'un triangle rectangle dont on connaît l'aire.
- Trouver deux nombres connaissant leur somme et leur produit
- R(X,Y,Z) = X3+Y3+Z3
- S(X,Y,Z) = X2 Y+X Y2+X Z2+X2 Z+Y2 Z+Y Z2
- T(X,Y,Z) = X4+Y4+Z4
A l'aide des polynômes symétriques élémentaires, on cherche les coefficients d'un polynôme du troisième degré dont ces trois nombres sont les racines.
Avec les notations ci-dessus, on réécrit le système :- d'où
- d'où
On écrit maintenant le polynôme P du troisième degré donné par les formules de Viète : , soit X3 - X2 - 10X +10 =0. Une racine évidente est x=1. Ensuite, soit on factorise P, soit on calcule la somme et le produit des deux autres racines pour écrire le facteur de degré deux dans P.
Pour la seconde méthode, de la première ligne du calcul des , et , on tire y+z=0 et de la deuxième y+z+y z = y z = -10. Les nombres y et z sont racines de X2-10.
Les solutions du système sont
Formule de Cardan
Résolution par radicaux d'une équation polynomiale
Ici nous montrons comment la résolution complète des équations du troisième degré, même à racines réelles, nécessite, dans certains cas, l'utilisation des nombres complexes. Ce problème est à l'origine de la définition des nombres complexes (voir Ensembles de nombres et équations ).
On sait résoudre les équations du second degré en utilisant des racines (carrées). On obtient des solutions dans ou dans . On peut se poser la question de savoir si l'on peut résoudre des équations de degré supérieur : 3, 4, 5, 6... en écrivant les solutions avec des racines (carrées, cubiques, etc.). La théorie de Galois répond que c'est possible pour les degrés 3 et 4 et impossible au-delà.
Étude du degré 3
Pour les équations de degré 3 à coefficients réels, les solutions sont données par les formules de Cardan. La forme générale d'une l'équation de degré 3 est : a x3+b x2+c x+d=0 avec réels et .
Réduction du terme en x2
Pour simplifier la tâche, on peut aisément éliminer le terme en x2 en divisant par a, puis en posant , ce qui conduit à une nouvelle équation équivalente de la forme : z3+p z+q = 0 avec ( p , q) dépendant de a,b,c,d. C'est un calcul simple à faire.
Introduction des inconnues u et v
La suite passe par une idée, due aux mathématiciens Cardan et Tartaglia, celle de chercher des solutions de la forme z=u+v (en se gardant, comme on le verra, la possibilité de préciser encore u et v), puis de se ramener à une équation du second degré.
En posant z=u+v, on peut écrire :
On fait alors le choix de poser . Ceci implique alors de résoudre le système :
Nous parlons d'implication et pas d'équivalence, ce qui impliquera quelques précautions qui seront examinées en dessous...
On pose alors U=u3 et V=v3. On a alors fait apparaître les valeurs de U+V et de U V, par conséquent U et V sont les solutions de l'équation du second degré (Et) : dont le discriminant est
Formule de Cardan dans le cas
Si 4p3+27q2 est strictement positif, le polynôme z3+p z+q admet au moins la racine réelle
On peut aussi l'écrire sous la forme :
Dans le cas , les solutions de (Et) sont : , c'est-à-dire, par exemple, puisque u et v jouent des rôles symétriques :
et
On peut ensuite calculer u et v, en prenant leurs racines cubiques (on est ici dans , un nombre n'a qu'une seule racine cubique) et ensuite z=u+v. Réciproquement, les valeurs trouvées pour u et v vérifient et u+v est bien solution de l'équation.Commentaires sur la formule de Cardan
Et les autres solutions ?
La formule de Cardan établie dans ne fournit qu'une seule racine réelle (alors qu'il peut en exister trois), et ceci uniquement si 4p3+27q2 est strictement positif. Si on raisonne dans , alors les valeurs de U et V trouvées dans la démonstration de cette page ont chacune trois racines cubiques, réelles ou complexes u,j u,j2 u pour U et v,j v,j2 v pour V ce qui fait neuf choix possibles pour le couple (u,v). On a mentionné plus haut une implication qui n'est pas une équivalence et on a trouvé neuf candidats solutions dont toutes ne peuvent pas convenir.
Pour trouver les "bonnes" solutions, il suffit les tester dans l'équation... Cette vérification en élimine six, il reste trois choix pour les racines de U et de V qui fournissent des solutions à l'équation. Les voici :
La première est réelle, et les deux autres sont complexes conjuguées du fait de et .
Lorsque 4p3+27q2 est strictement positif, on peut calculer une racine réelle du polynôme en se limitant à , et, dès lors que l'on connaÎt , ensemble inconnu par Cardan et Tartaglia, les deux autres racines qui sont conjuguées.
C'est la résolution complète par radicaux de l'équation de degré 3 dans le cas où
.
Notons que la formule de Cardan permet ici de trouver la racine réelle, mais que la connaissance
des deux autres (complexes conjuguées) nécessite la connaissance de
.
Le cas
va permettre une introduction de
...
Que se passe-t-il si 4p3+27q2 est strictement négatif ?
Un calcul osé dans un exemple
L'application de la formule de Cardan par Bombelli, mathématicien du XVI-ième siècle, à l'équation z3-15z-4=0 (qui possède une racine facile à deviner : z0 = 4) conduit à . Une impasse à cette époque où les nombres complexes n'ont pas encore été introduits. À cette racine de -1 qui n'existe pas, Bombelli ose donner un nom (ce nom sera définitivement établi par Euler) : disons i, (début d'imaginaire !) avec , cette racine s'écrit (continuons d'oser!) . Il est alors assez facile de vérifier, ce que Bombelli fait avec ses règles de calcul, que :
et
autrement ditet
On obtient alors ... et on retrouve la racine connue de l’équation ! Les calculs "osés" de Bombelli ont permis de retrouver le résultat. Historiquement, c'est ce qu'on appelle une coupure épistémologique dans la science, qui ouvre la voie à l'introduction des nombres complexes...
Traitement du cas 4p3+27q2 < 0
On suppose connue maintenant l'existence de . On reprend la démonstration de la formule de Cardan dans le cas où 4p3+27q2 est strictement négatif. Alors on écrit et le résultat de la résolution de l'équation (Et) devient :
et .
On remarque que V et U sont conjugués et on obtient à nouveau 9 couples (u,v) , avec . Là encore, trois seulement sont solutions, les autres étant éliminés après test dans l'équation :
Lorsque 4p3+27q2 est strictement négatif, on peut calculer les trois racines réelles du polynôme en utilisant les nombres complexes.
Transformation de Fourier discrète (TFD)
La transformation de Fourier discrète (TFD) est un outil mathématique de traitement du signal numérique. Elle utilise des fonctions exponentielles complexes, raison de la présence de ce chapitre ici. On en présentera ici une approche simple, limitée à des fonctions périodiques (voir ce cours sur les fonctions périodiques ).
Problème
Donnons un aspect rapide du problème. On appelle signal une quantité dépendant du temps. Une fonction, la courbe des cours de la Bourse, un enregistrement météo, un son ... Certains de ces signaux sont périodiques.
Exemple de fonction périodique : La fonction de la variable t (le temps) et de période T avec représentée par la courbe ci-dessous est définie par pour , et par périodicité ailleurs.

A la notion de période T, on ajoute les notions (vues en physique) de fréquence f et celle de pulsation d'un phénomène périodique. Ces notions sont reliées par les relations : .
Analyse du problème
Pour comprendre les étapes, mais sans trop rentrer dans les détails, on peut donner l'exemple de l'enregistrement, puis la restitution d'une musique à l'aide d'un CD. L'enregistrement se fait avec un micro, c'est un processus analogique. L'écoute se fait avec des hauts parleurs, c'est également un processus analogique. Entre les deux, le son doit être transformé, il est analysé et numérisé. La TFD permet de relier les intensités du son aux fréquences des éléments (harmoniques) qui le constituent
Soit s un signal, périodique de période T. La fréquence fondamentale du signal est .
Si on fait tracer la courbe de s sur un écran, on obtient une courbe continue ou continue par morceaux dont l'équation est en général inconnue. Nous indiquons à cette page un théorème hors programme affirmant que, sous de bonnes hypothèses, la fonction s peut être approchée par une fonction somme de cosinus ou de sinus.
Analyse temporelle par l'échantillonnage
Afin de diminuer la complexité des calculs sur un signal, on recourt à deux simplifications indiquées ci-dessous : c'est le principe de l'échantillonnage.
- On se limite à un intervalle de temps borné, par exemple une période , que l'on divise en N intervalles de temps ( N entier) : .
- En chacun des instants ti ), on mesure les intensités prises par le signal. On obtient ainsi une suite .
Ce processus est l'analyse temporelle du signal qui a été ainsi échantillonné par la suite . Pour rendre compte de la complexité d'un signal ou de la richesse de ses harmoniques il faut que N soit très grand. Pour donner un ordre d'idée, le son reproduit par un CD est échantillonné fois par seconde.
Le dessin de gauche, ci-dessous, représente la courbe d'un signal (ici ), celui de droite montre un échantillonnage, une numérisation de la courbe. Les valeurs xi sont les ordonnées des extrémités supérieures des segments rouges.


Analyse fréquentielle
Le signal (son) est, comme on le voit dans le théorème , la somme de ses harmoniques. Ces harmoniques sont associés à des fréquences fk multiples de la fréquence fondamentale f1 et on souhaite pouvoir représenter ces fréquences ainsi que l?importance de chacune d'entre elles. Le résultat de ce travail sera une courbe du type de celle figurant au bas de cette page (courbe "en peigne"), où chaque fréquence fk est repérée en abscisse par une barre dont la hauteur correspond à son importance.
[En fait, dans la pratique, plutôt que d'utiliser des sommes de fonctions trigonométriques, il est plus commode d'utiliser des sommes de fonctions exponentielles complexes de type avec , sachant que le lien trigonométrique/exponentielle se fait par les formules d'Euler. ]
La transformation de Fourier discrète (TFD) permet d'arriver à ce résultat, en calculant, à partir de la suite , une suite où les valeurs représentent la part de la fréquence fk dans le signal.
Aux nombres complexes
on associe les fréquences
.
La suite
(
) constitue le spectre des fréquences qui complète
l'analyse temporelle
obtenu par l'échantillonnage.
On verra à la
page suivante
une illustration de ces résultats.
Lorsque le nombre N d'échantillons est suffisamment grand, le spectre des fréquences se rapproche du spectre harmonique du signal, c'est-à-dire de l'ensemble des harmoniques inclus dans le son et qui lui donnent sa richesse. Voici ci-dessous un exemple de spectre des fréquences.

Exemples et exercices sont en page suivante TFD : Définition, exemples, exercices .
Théorème d'approximation d'un signal
L’éventuelle complexité de ce qui suit autorise à n'en lire que les cinq dernières lignes : le résultat principal. On admet donc le théorème suivant :
Soit K un entier. Toute fonction, tout signal périodique, suffisamment régulière, où t est le temps, peut être approchée (et ceci d'autant mieux que K est grand) par une fonction somme de cosinus sous la forme :
.
Cette video La formule de Joseph Fourier. Du sinus de l'antiquité aux fichiers mp 3 de Canal U illustre bien ce théorème.
Diverses définitions.
Les nombres
ck et
sont des constantes,
f1 la fréquence fondamentale du signal. On note
.
Le terme de rang
k :
s'appelle
l'harmonique de rang
k du signal. Il est défini par son amplitude
ck
et son décalage de phase
(qui ne nous intéresse pas ici).
Avec ces notations la fonction s'écrit :
Plus K est grand, plus , la somme des harmoniques, est proche du signal s.
TFD : Définition, exemples, exercices
Cette page propose des exemples et exercices de calcul de la TFD ainsi qu'un bref alinéa sur une application.
Soit N un entier supérieur ou égal à 1 et une suite de N valeurs . On pose, pour :
On appelle transformation de Fourier discrète (TFD) la transformation définie par :
TFD
Transformée de Fourier discrète de la série (0,1,0).
On calcule :- X0 = x0+x1+x2
Calcul de la TFD d'un signal sur une fenêtre I découpée en quatre intervalles
Valeurs du signal t -> x(t)
Dénominateurs
Fonction signal E [ t --> x(t) ]
Courbe du signal t -> x(t)
Valeurs de la fonction spectrale u -> X(u)
} }
Fonction spectrale : modules T_0,T_1,T_2,T_3 de X_0,X_1,X_2,X_3
Parties réelle et imaginaire avec 2décimales
Fonction spectrale F [ u --> X(u) ]
Courbe du spectre k -> X(k)
Tableau des 2 courbes
|
et
N = 4 4 intervalles de 0 à 4 4 échantillons t0=0, 2,1,2,3,20 = 2, t1=1, 2,1,2,3,21 = 1, t2=2, 2,1,2,3,22 = 2, t3=3, 2,1,2,3,23 = 3 |
||||
| Courbe du signal : | Spectre : |
Remarques.
- L'échantillonnage est visualisé sur la courbe de gauche par les pointillés rouges. Le spectre des fréquences est représenté à droite par les barres verticales bleues. La courbe spectrale représentée en pointillé bleu n'a pour cet exercice que peu de sens, elle ne devient significative que si le nombre N d'échantillons est suffisamment grand.
- Pour simplifier, les graduations de l'axe des abscisses de chacune des figures ci-dessus ont été ramenées par des changements d'échelles aux valeurs 0,1,2,3 qui sont de simples numéros.
- En réalité, on échantillonne la fonction avec en abscisse les N valeurs suivantes : .
- X0 = 2+1+2+3 = 8
Applications de la TFD au traitement du signal
Dans un système électronique (S), un signal-entrée : à l'entrée d'une boîte noire en ressort sous la forme d'un signal-réponse . Il est souvent instructif de comparer les spectres de fréquences entrée et sortie en faisant varier la forme et les paramètres du signal-entrée, pour obtenir un résultat souhaité.En Électronique notamment, la TFD permet d'adapter les caractéristiques du système (S) dans le but d'obtenir un spectre du signal-réponse de type donné.
Ensemble de Mandelbrot, quelques résultats.
On appelle ensemble de Mandelbrot, noté M, l'ensemble des nombres complexes c pour lesquels cette suite est bornée.

Cet ensemble M est la célèbre fractale de Mandelbrot représentée en noir dans la figure ci-dessus. La propriété d'un objet fractal est d'avoir la même structure à toute échelle. Consulter cette page Wikipedia.
Quelques résultats à démontrer.
Pour ces démonstrations, l'inégalité triangulaire sous sa forme complète sera utile, et on l’utilisera parfois avec des inégalités dans l'autre sens :
- Montrer pour tout
n dans
l'égalité :
.
En déduire que l'ensemble des images dans le plan complexe des nombres
c tels que
c appartienne à
M est symétrique
par rapport à l’axe des abscisses. Dorénavant, on notera
zn(c) = zn.
Solution. On procède par récurrence. L'hypothèse de récurrence, à un rang n, est : . L'initialisation est immédiate, est vraie. Pour l'hérédité, montrons que est vraie : De , on peut écrire, grâce à l'hypothèse de récurrence et aux propriétés du module et du conjugué,
.
Donc est vraie, ainsi que , d'où le résultat..Par ailleurs, si la suite est bornée, alors l'est aussi, ainsi que . On en déduit que si , alors . En d'autres termes l'ensemble des images dans le plan complexe des nombres c tels que c appartienne à M est symétrique par rapport à l'axe des abscisses.
- Calculer
z1,
z2 et
z3. Montrer que
zn s'écrit comme un polynôme en
c. Quel est son degré ?
Solution. On calcule- z1 = c, z2= c2+c, z3= c4+2c3+c2+c.
- Par récurrence. z1 est un polynôme. Supposons que zn le soit. Alors . Le carré d'un polynôme est aussi un polynôme. Donc également. D'où le résultat.
- Sur les premières valeurs, il semble que l'on puisse faire l'hypothèse que, pour le degré de zn est (hypothèse de récurrence). C'est vrai pour n=1 et n=2. Supposons le résultat vrai au rang n. Le degré de est le double de celui de zn, il est égal à . D'où le résultat.
-
Soit
p un entier naturel et
une suite non constante. On dit qu'elle est stationnaire
à partir de
zp si les deux conditions suivantes sont vérifiées :
- pour tout l'égalité zp = zn est vérifiée.
- Si , zp est différent de .
- Montrer que si, pour un entier naturel
q, on a
, alors tous les termes d'indice supérieur
à
q (
zq et les suivants) sont tous égaux à
zq.
Solution. On considère la propriété : Pour tout . Elle est initialisée au rang q. Alors de , on tire et, par définition de la suite, . C'est ce que l'on voulait démontrer. En résumé, est vraie et pour tout . En conclusion, la suite est stationnaire à partir de zq.
- Donner une condition nécessaire et suffisante pour que tous les termes de la suite
soient nuls. La suite peut-elle être stationnaire à partir de
z1 ?
Solution.
Si les termes de la suite sont nuls alors c=0. Réciproquement, si c est nul, tous termes de la suite sont nuls.
Conclusion : la suite est la suite nulle si et seulement si c est nul.
Si la suite est stationnaire à partir de z1, alors z0=0, z1=c, z2 = c2+c = z1=c. Donc c est nul, et la suite est la suite nulle. Elle ne peut donc pas être stationnaire à partir de z1.
- Montrer que si deux termes consécutifs de la suite sont nuls alors tous les termes de la suite sont nuls.
Solution. Soit un entier naturel q tel que . Alors de , on tire c= 0. Or, si c est nul, d'après la question précédente, la suite est la suite nulle.
- On suppose maintenant que
c est non nul et
p supérieur ou égal à
2. Montrer que la suite
est stationnaire à partir de
zp si et seulement si
.
Solution.
Supposons d'abord : . Alors on a :
.
On conclut à l'égalité de tous les termes à partir de p comme en (i) et comme et -zp sont opposés et non nuls ensemble (voir (iii)), la deuxième condition de la définition est vérifiée.
Réciproquement, supposons maintenant la suite stationnaire à partir de zp. On a les implications suivantes grâce à la définition de la suite :
.
Puisque la suite est stationnaire à partir du rang p+1, la condition (b) s'écrit et on obtient l'égalité
- La suite peut-elle être stationnaire à partir de
z2? Quelle est cette suite ?
Solution.
Par définition, z0 = 0, z1 = c, z2 = c2+c. On utilise la caractérisation de la question précédente : z1+z2=0, dont on tire z2= -c et donc c2+c= -c, soit c2+2c=0.
L'équation c2+2c=0 a deux solutions : c=0 (pour cette valeur, on a vu que la suite est nulle) et c= -2. Pour c= -2, les termes sont (). La suite est stationnaire à partir de z3 et prend ensuite la valeur 2.
- On suppose dans cette question que
p est la plus petite valeur de
n telle que la suite
soit 2-périodique (et non stationnaire) à partir de
zp,
c'est-à-dire vérifie
.
Le suite
peut-elle être 2-périodique à partir de
z0 ? Donner ses valeurs. Mêmes questions à partir de
z2.
Solution.
- Si la suite est 2-périodique à partir de z0, alors, z0=0, z1=c, z2=c2+c=0... Deux valeurs conviennent c=0 (exclus, la suite est nulle) et c= -1. Dans ce dernier cas, la suite est bien 2-périodique (Vérifiez-le). Les termes sont : .
- Si la suite est 2-périodique à partir de z2. Alors on reprend les résultats de la question 2 et on calcule z4 = z32+c = (c4+2c3+c2+c)2 +c ; par périodicité, on obtient l'équation : (c4+2c3+c2+c)2 +c =c2+c La résolution de cette équation (à la main (faisable) ou avec un logiciel de calcul !) fournit (en dehors de 0) 4 solutions : {}
- Dans le cas c = -2, on a vu à la question précédente que la suite est stationnaire à partir de z2. On rejette donc cette valeur.
- Dans le cas c= -1, on a vu au début de cette question que la suite est 2-périodique, mais à partir de z0. On rejette donc cette valeur.
- Dans le cas , cette valeur convient et les termes de la suite sont :
- Dans le cas , cette valeur convient et les termes de la suite sont :
- On va montrer que
M est inclus dans un cercle de centre
O. On suppose
.
Prouver que pour tout
, on a les résultats suivants :
-
Solution. Par récurence. Pour . Hérédité : on suppose qu'à un rang n on a : , et on va utiliser la partie de l'inégalité triangulaire :
et la définition de la suite pour écrire cet enchaînement d'inégalités :
On en déduit donc l'inégalité . -
Solution. On peut écrire pour :
-
.
Solution. Preuve à nouveau par récurrence. Il est facile de voir que la propriété est vraie pour n=1, puisqu'on a . Supposons la propriété vraie au rang n. Alors, au rang n+1, on utilise le résultat précédent (voir (iii)) :
Ce qui achève la preuve. - Montrer maintenant que
M est inclus dans un cercle de centre
O.
Solution. Dans le cas , on a : donc, d'après la question précédente, on en déduit () et la suite n'est pas bornée ; donc c n'appartient pas à M.
Conclusion : est ainsi une condition nécessaire pour que la suite (zn) soit bornée. L'ensemble M est donc inclus dans le cercle de centre O d'affixe 0 et de rayon 2.
-