Graphes
Graphes
I Graphes simples
Graphes
→ I Graphes simples
I-3 Sous-graphes, le théorème de Turán
I-1 Définitions
Graphes
→
I Graphes simples
→ I-1 Définitions
On dit que deux sommets et sont voisins si est une arête. Le nombre de voisins du sommet est appelé son degré et est souvent noté . Un sommet isolé est un sommet de degré 0, c'est-à-dire sans voisin.
Donnons tout de suite un résultat fondamental
Théorème
Le nombre d'arêtes d'un graphe simple est égal à la demi-somme des degrés de ses sommets:
Démonstration
Notons
l'ensemble des bouts, couples
tels que
. Comme chaque arête a deux bouts, on a
par le principe des bergers. D'autre part, chaque sommet
appartient à
arêtes. On a donc
, d'où le résultat.
En conséquence
Corollaire
Le nombre de sommets de degré impair d'un graphe simple est pair.
On utilise souvent des raccourcis, parlant du graphe plutôt que de ses sommets ou de ses arêtes. Par exemple, le degré minimum, respectivement maximum, du graphe
est défini comme
respectivement
Si ces deux nombres sont égaux, c'est-à-dire si tous les sommets ont le même degré , on dit que le graphe est -régulier.
Une représentation plane du graphe est un dessin plan, comportant points étiquetés par les éléments de et pour chaque arête , une courbe simple, par exemple un segment de droite, joignant les sommets étiquetés et . Les croisements entre ces représentations des arêtes ne sont pas significatifs. Toutefois, il est souvent préférable de les éviter si possible. Un graphe planaire est un graphe qui admet une représentation plane sans croisement, mais cette notion ne jouera pas un rôle central dans ce cours. Voici deux représentations du graphe
 et
et

Un isomorphisme du graphe simple sur le graphe simple est une bijection telle que
Il est facile de voir que cela définit une relation d'équivalence sur les graphes. Par exemple, il y a graphes distincts dont l'ensemble des sommets est :












I-2 Bestiaire
Graphes
→
I Graphes simples
→ I-2 Bestiaire
- Le
-stable
, ou stable d'ordre
est un graphe d'ordre
sans arête. Voici
:

- La
-clique, ou graphe complet d'ordre
est un graphe d'ordre
dans lequel deux sommets distincts sont toujours voisins.
Voici
:

- La
-chaîne
ou chaîne de longueur
a pour
ensemble de sommets
(c'est donc un graphe d'ordre
), avec
voisin de
si et seulement si
. Voici
:

- Le
-cycle
ou cycle de longueur
a pour
ensemble de sommets
(c'est donc un graphe d'ordre
), avec
voisin de
si et seulement si
ou
.
Voici
:
 ou encore
ou encore

- Soit
un entier. Le
-cube
, ou cube de dimension
est un graphe dont les sommets sont
les chaînes de caractères de longueur
sur l'alphabet
. Deux sommets sont voisins dans le graphe si et seulement si les chaînes correspondantes diffèrent en une seule
position. Voici
:
 ou
ou

- Le graphe de Petersen est le graphe suivant:

I-3 Sous-graphes, le théorème de Turán
Graphes
→
I Graphes simples
→ I-3 Sous-graphes, le théorème de Turán
Le graphe complémentaire du graphe simple est un graphe qui a les mêmes sommets que , mais dans lequel deux sommets distincts sont voisins si et seulement si ils ne le sont pas dans . En d'autre termes, on a . Un graphe est auto-complémentaire si et seulement si il est isomorphe à son complémentaire. Les deux figures plus haut pour et montrent que est auto-complémentaire.
Un sous-graphe d'un graphe simple est un graphe tel que et . On dit que c'est un sous-graphe couvrant si . Pour toute partie de , on définit le sous-graphe de induit par et on note le graphe , où est l'ensemble des arêtes de dont les deux extrémités sont dans .
On dit que contient le graphe s'il existe un sous-graphe de isomorphe à . Nous allons prouver le
Théorème [de Turán]
Soit
et
des entiers. Si le graphe simple
d'ordre
ne contient pas de
-clique, alors
Démonstration
Par récurrence sur
et
. Pour
ou
, il n'y a rien à démontrer. Soit donc
et
deux entiers, et supposons le résultat vrai pour
ou
. On considère un graphe simple
d'ordre
qui ne contient pas de
-clique.
Si ne contient pas de -clique, on peut appliquer l'hypothèse de récurrence avec . On a donc
Si ne contient pas de -clique, on peut appliquer l'hypothèse de récurrence avec . On a donc
Nous pouvons donc supposer que contient une -clique, c'est-à-dire qu'il existe une partie de de cardinal telle que tous les éléments de sont voisins entre eux. Notons . Si est vide, le graphe est la clique , on a et
Sinon, le graphe induit ne contient pas non plus de -clique et a un ordre . On peut lui appliquer l'hypothèse de récurrence et on a
Les arêtes de sont de trois sortes: celles qui ont leurs deux extrémités dans , au nombre de , celles dont les deux extrémités sont dans , au nombre de majoré ci-dessus, et celles dont une extrémité est dans et l'autre dans . Pour chaque sommet de , il y a au moins un sommet de qui n'est pas voisin de , puisque autrement serait une -clique de . Il y a donc au plus arêtes de la troisième espèce qui ont pour extrémité, et il y a au plus arêtes de troisième espèce en tout. Au total, on a
On remarque que si est un multiple de , on peut construire un graphe d'ordre de la façon suivante: on répartit les sommets en groupes de éléments et deux sommets quelconques sont voisins si et seulement si ils n'appartiennent pas au même groupe. Voici l'exemple , :

Il est clair que ce graphe ne contient pas de -clique puisque d'après le principe des tiroirs toute partie de de cardinal contient deux sommets de même groupe, donc non voisins. Comptons les arêtes du graphe. Il y a paires de groupes et arêtes entre éléments de cette paire de groupes. On a donc
et la borne donnée par le théorème de Turán est atteinte.
I-4 Colorations
Graphes
→
I Graphes simples
→ I-4 Colorations
Une application de l'ensemble des sommets d'un graphe simple est une coloration du graphe si l'image par d'une arête est toujours un ensemble à 2 éléments. On appelle couleur du sommet l'élément de et la condition s'exprime sous la forme ``Si deux sommets sont voisins, ils sont de couleurs différentes''.
Le plus souvent, on ne s'intéresse pas aux couleurs, mais seulement à la répartition des sommets en couleurs distinctes. Les sommets d'une couleur donnée forment un stable de , c'est-à-dire une partie de qui ne contient aucune paire de sommets voisins. Si , on dit que la coloration utilise couleurs. Les ensembles de sommets des différentes couleurs forment une partition de en stables. On dit que le graphe est -parti (biparti pour , triparti si , etc.) s'il existe une telle partition, ou encore s'il existe une coloration de qui utilise exactement couleurs. Nous verrons plus loin une caractérisation simple des graphes bipartis.
Nous ajoutons ici un spécimen dans notre bestiaire. Soit un entier et une famille d'entiers non nuls. On définit le graphe multiparti complet de la manière suivante. L'ensemble des sommets a éléments. Il est partitionné en parties , avec pour tout . Deux sommets sont voisins si et seulement si ils n'appartiennent pas à la même partie. C'est, bien sûr, un graphe -parti. Le graphe est représenté plus haut dans la discussion du théorème de Turán. Voici une représentation de

Il est clair que l'application identique est une coloration de qui utilise couleurs. Il est alors naturel de se demander combien de couleurs sont nécessaires pour colorier un graphe . Le nombre chromatique du graphe est le plus petit entier pour lequel il existe une coloration de utilisant couleurs. La proposition suivante donne les nombres chromatiques associés aux graphes vus plus haut.
Proposition
- si et seulement si est un -stable,
- si et seulement si est une -clique,
- pour ,
- pour ,
- ,
- .
La preuve de cette proposition sera faite en exercice.
À chaque numérotation des sommets, on fait naturellement correspondre une coloration par des entiers naturels non nuls grâce à l'algorithme glouton:
pour i allant de 1 à n faire colorier le sommet i avec la première couleur parmi 1,2,3... qui n'est pas déjà utilisée par un voisin du sommet i fin faire
Ainsi, le sommet est colorié avec la couleur 1, le sommet est colorié avec la couleur 2 s'il est voisin de et avec sinon, etc. Dans la figure suivante, nous avons appliqué cet algorithme deux fois au même graphe, mais avec des numérotations différentes des sommets. Entre parenthèses les numéros des couleurs sont indiqués. On voit que la première numérotation utilise 4 couleurs en tout alors que la deuxième en utilise 5. On peut montrer qu'il existe toujours une numérotation des sommets telle que l'algorithme glouton utilise couleurs, mais cela n'a rien d'évident.


Rappelons que nous avons défini le degré maximum d'un graphe comme le maximum des degrés des sommets de . On a la
Proposition
Le nombre chromatique d'un graphe simple vérifie
Démonstration
En fait, quel que soit l'ordre choisi sur les sommets, l'algorithme glouton utilise au maximum
couleurs distinctes. Soit en effet
le numéro de la plus haute couleur utilisée, et
un sommet qui a cette couleur. L'algorithme glouton attribue la couleur
à
parce que les voisins de
déjà coloriés occupent toutes les couleurs de
à
. Donc
a au moins
voisins distincts, et
, d'où
.
I-5 Graphes planaires
Graphes
→
I Graphes simples
→ I-5 Graphes planaires
On rappelle qu'un graphe est planaire s'il admet une représentation plane dans laquelle les courbes qui représentent les arêtes ne se croisent pas. On dit que le graphe est un mineur du graphe si on peut obtenir un graphe isomorphe à à partir de en effectuant une suite d'opérations dont chacune est de l'un des trois types suivants:
- ablation d'une arête
- ablation d'un sommet et de toutes les arêtes dont ce sommet est une extrémité.
- suture d'une arête: on identifie les deux extrémités de l'arête, et on efface la boucle et les arêtes multiples qui découleraient de cette identification.

On peut montrer qu'un graphe est planaire si et seulement si ni ni ne sont des mineurs de .
Considérons une carte de géographie, divisée en un certain nombre de pays d'un seul tenant. On lui associe un graphe de la manière suivante: dans chaque pays, on met un sommet, et les sommets associés à deux pays sont voisins si ces pays ont une frontière commune --- pas seulement un point commun, une certaine longueur de frontière. Aux deux cartes suivantes,


on associe donc les deux graphes suivants:


Le graphe obtenu est planaire, et à une coloration de ce graphe on associe un coloriage de la carte dans lequel deux pays limitrophes ont des couleurs différentes.
En 1976, Appel et Haken ont démontré le
Théorème [des quatre couleurs]
Toute carte de géographie plane peut être coloriée avec quatre couleurs de façon que deux pays limitrophes aient toujours des couleurs différentes.
Les considérations ci-dessus montrent que cet énoncé est équivalent au suivant:
Théorème
Si
est un graphe simple planaire,
.
La démonstration a fait sensation à l'époque, non seulement parce que le problème datait de plus d'un siècle, mais aussi parce qu'elle se décomposait en environ 1500 cas, ce qui avait rendu nécessaire d'en faire écrire et vérifier une partie essentielle par des machines.
II Multigraphes
Graphes
→ II Multigraphes
Un multigraphe est la donnée d'un couple d'ensembles finis, avec non vide, ainsi que d'une application qui à chaque arête fait correspondre un ensemble de 1 ou 2 sommets, ses extrémités. Si est un singleton, on dit que l'arête est une boucle de base . On parlera en général du multigraphe , en oubliant la fonction . Les représentations des multigraphes utilisent des lignes courbes. Voici un exemple de multigraphe

À tout multigraphe , on fait correspondre le graphe simple sous-jacent , où
en d'autres termes, on efface les boucles et on consolide les arêtes multiples en une seule. Le graphe simple sous-jacent au multigraphe ci-dessus est donc

Dans toute la suite, nous utiliserons le terme graphe pour désigner un multigraphe, pour signifier qu'en réalité la situation ne concerne que le graphe simple sous-jacent.
On définit de façon naturelle un isomorphisme entre et comme un couple , où est une bijection de sur , est une bijection de sur telle que
Un sous-graphe d'un multigraphe est un multigraphe tel que , et . Un tel sous-graphe est couvrant si . Le sous-graphe induit par est le multigraphe , avec
On peut encore dire qu'un multigraphe en contient un autre s'il admet un sous-graphe isomorphe à cet autre. Par exemple, le multigraphe contient

II-1 Matrices d'incidence et d'adjacence
II-2 Chaînes dans un multigraphe
II-3 Algorithmes de Moore et de Dijkstra
II-1 Matrices d'incidence et d'adjacence
Graphes
→
II Multigraphes
→ II-1 Matrices d'incidence et d'adjacence
La matrice d'incidence du graphe est une matrice définie par
La somme des éléments de la colonne d'indice vaut 2. La somme des éléments de la ligne est, par définition, le degré de : les boucles de base comptent pour 2, les autres arêtes d'extrémité pour 1. On peut alors énoncer la même relation fondamentale que pour les graphes simples:
Théorème
Le nombre d'arètes d'un multigraphe est égal à la demi-somme des degrés de ses sommets:
Démonstration
Ce nombre est égal à la somme de tous les éléments de la matrice
:
Et on a encore le
Corollaire
Le nombre de sommets de degré impair d'un multigraphe est pair.
La matrice d'adjacence du graphe est une matrice définie par
On voit que cette matrice est symétrique. La somme des éléments d'une ligne (ou colonne) n'est pas le degré du sommet correspondant puisque les boucles ne sont ici comptées qu'une fois.
Voici les matrices d'incidence et d'adjacence du multigraphe dessiné plus haut.
II-2 Chaînes dans un multigraphe
Graphes
→
II Multigraphes
→ II-2 Chaînes dans un multigraphe
Soit un entier naturel. Une -chaîne, ou chaîne de longueur d'un multigraphe est la donnée d'une famille de sommets et d'une famille de arêtes telles que pour tout , on ait . On note
On dit que la chaîne
 visite chacun des
et des
.
Le sommet
est l'origine de la chaîne
visite chacun des
et des
.
Le sommet
est l'origine de la chaîne
 et
est son extrémité.
En particulier, si
est un sommet,
est une
-chaine, d'origine
et extrémité
.
Une chaîne est fermée si
. Elle est simple si les arêtes
sont distinctes. Elle est élémentaire si les sommets
sont distincts.
et
est son extrémité.
En particulier, si
est un sommet,
est une
-chaine, d'origine
et extrémité
.
Une chaîne est fermée si
. Elle est simple si les arêtes
sont distinctes. Elle est élémentaire si les sommets
sont distincts.Dans un graphe simple, on a forcément . On se contente donc de noter les sommets et on écrit .
Il y a des opérations naturelles sur les chaînes: Si l'extrémité de est égale à l'origine de , c'est-à-dire si , on peut définir la concaténation
en posant et pour . On peut aussi définir la chaîne
qui est ``
 parcourue dans l'autre sens'' en posant
et
.
parcourue dans l'autre sens'' en posant
et
.Théorème
Soit
un multigraphe, et
sa matrice d'incidence. Pour tout
et tout couple
, le coefficient
de la puissance
-ième de
est égal au nombre de
-chaînes d'origine
et extrémité
.
Démonstration
Par récurrence sur
. La matrice
est la matrice identité
, et il est clair que le nombre de 0-chaînes d'origine
et extrémité
vaut 1 si
et 0 sinon. La propriété est donc vraie pour
. Supposons-la vraie pour
. Une
-chaîne d'origine
et extrémité
s'écrit
, avec
et
. Si
,
est une
-chaîne d'origine
et extrémité
et
vérifie
. L'hypothèse de récurrence dit qu'il y a
possibilités pour la première partie et la définition de
dit qu'il y a
possibilités pour la seconde.
Le nombre de
-chaînes d'origine
, extrémité
et telles que le sommet
soit
vaut donc
. le nombre total de
-chaînes d'origine
et extrémité
est donc
II-3 Algorithmes de Moore et de Dijkstra
Graphes
→
II Multigraphes
→ II-3 Algorithmes de Moore et de Dijkstra
On définit une fonction appelée distance sur de la façon suivante. S'il existe une chaîne d'origine et extrémité , est la longueur minimale d'une telle chaîne. S'il n'en existe pas, on pose .
Cette fonction n'est pas une distance au sens usuel puisque elle peut prendre la valeur
 . Mais il est facile de voir que la fonction
. Mais il est facile de voir que la fonction
est une distance sur . Dans la pratique, on préfère utiliser , qui prend des valeurs entières.
Donnons un algorithme classique de calcul de , pour un sommet fixé et tout sommet , l'algorithme de Moore:
Données: Un sommet s d'un graphe (S,A) Sortie: Pour tout dans S, D[t] contient D(s,t)
D[s] <- 0 Pour tout t dans S faire D[t] <- infini fin pour k <- 0 V <- {s} (V est un ensemble de sommets, au départ un singleton) tant que V n'est pas vide faire k <- k+1 W <- {} (ensemble vide) pour tout x dans V faire pour tout y voisin de x et tel que D[y] = infini faire D[y] <- k W <- W union {y} (on ajoute y à l'ensemble W) fin pour fin pour V <- W fin tant que
En d'autre termes, est étiqueté 0, les voisins de étiquetés 1, les voisins des voisins de sauf lui-même sont étiquetés 2, et si est étiqueté , ses voisins non encore étiquetés seront étiquetés , etc. Voici un exemple d'exécution de l'algorithme de Moore

Il existe une généralisation naturelle de cette notion de distance sur un graphe. Un graphe valué est la donnée d'un multigraphe et d'une fonction appelée coût ou poids ou longueur... Le coût d'une chaîne est alors défini par . On définit la distance entre deux sommets d'un graphe valué comme le minimum des coûts des chaînes d'origine et extrémité s'il en existe, et
 s'il n'en existe pas. Pour déterminer
pour un sommet fixé
et chaque sommet
, on peut utiliser l'algorithme de Dijkstra:
s'il n'en existe pas. Pour déterminer
pour un sommet fixé
et chaque sommet
, on peut utiliser l'algorithme de Dijkstra:
Données: Un sommet s d'um graphe valué (S,A,m),
Sortie: Pour tout t dans S, C[t] contient C(s,t)
Si 0 < C[t] < infini, T[t] contient la première étape
dans une chaîne de coût minimal menant de t à s.
Pour tout t dans S faire
C[t] <- infini
fin pour
C[s] <- 0
V <- {} (ensemble vide)
W <- S (tous les sommets)
tant qu'il y a dans W un sommet t tel que C[t] est fini faire
u <- un sommet de W tel que C[u] soit minimal
V <- V union {u}
W <- W \ {u} (On transfère u de W vers V)
pour chaque voisin x de u faire
si C[u] + m({u, x}) < C[x] faire
C[x] <- C[u] + m({u, x})
T[x] <- u
fin si
fin pour
fin tant que
Pour montrer que cet algorithme est correct, il suffit de vérifier que l'invariant de boucle suivant est maintenu: si est dans V, un chemin de moindre coût de à commence par T[t] est reste dans V. On peut montrer que la complexité de cet algorithme est en , où est le nombre de sommets et le nombre d'arêtes.
Voici par exemple les étapes de l'algorithme sur une valuation du cube .

Les étiquettes des sommets représentent le tableau C et le tableau T est représenté par des flèches qui pointent de t vers T[t]. Si un sommet est dans V, le point qui le marque est plus gros.









Pour trouver comment rejoindre le coin en bas à gauche à moindre coût, suivre les flèches.
III Chaînes et cycles
Graphes
→ III Chaînes et cycles
III-1 Connexité
Graphes
→
III Chaînes et cycles
→ III-1 Connexité
Théorème
La relation
est une relation d'équivalence sur
.
Démonstration
Elle est
- réflexive puisque est une 0-chaîne d'origine et extrémité .
- symétrique puisque si
 a pour origine
et extrémité
, alors
a pour origine
et extrémité
.
a pour origine
et extrémité
, alors
a pour origine
et extrémité
.
- transitive puisque si
 a pour origine
et extrémité
, et
a pour origine
et extrémité
, et
 a pour origine
et extrémité
, alors
a pour origine
et extrémité
.
a pour origine
et extrémité
, alors
a pour origine
et extrémité
.
Un graphe sera dit connexe si deux sommets quelconques sont toujours reliés. Il revient au même de dire que ne prend que des valeurs finies, ou encore que le diamètre du graphe est fini.
À toute relation d'équivalence sur un ensemble , on associe une partition de en classes d'équivalence. On a donc une partition . Si deux sommets sont voisins, ils sont reliés. Toute arête de relie donc deux sommets qui appartiennent à la même classe. En posant , on a donc montré que est réunion disjointe des . Les multigraphes ont la propriété que deux sommets quelconques de sont reliés dans . Ils sont donc connexes, et on a montré le
Théorème
Pour tout graphe
, il existe une partition unique de
en
parties non vides telle que les sous-graphes induits
soient connexes et que toute arête de
appartienne à un des
.
Les sont appelés les composantes connexes de et est le nombre des composantes connexes de . La fonction induit une distance sur chaque composante connexe de . Il est facile de voir que tous les graphes du bestiaire sont connexes, sauf le stable pour , qui a composantes connexes.
Théorème
Un graphe
est connexe si et seulement si pour toute partition de
en 2 parties (non vides)
et
, il existe une arête
dont une extrémité est dans
et l'autre dans
.
Démonstration
Suppossons d'abord
connexe. Considérons une partition
en 2 parties (non vides)
et
. Comme
et
sont non vides, on peut choisir
et
. Comme
est connexe, il existe une chaîne
d'origine
et extrémité
. L'ensemble
n'est pas vide puisque
, et ne contient pas
puisque
. Notons
son plus petit élément. On a
, donc
et
. L'arête
a une extrémité dans
et une autre dans
.
Réciproquement, supposons que pour toute partition de en 2 parties (non vides) et , il existe une arête dont une extrémité est dans et l'autre dans . Considérons deux sommets et de . Notons l'ensemble des extrémités des chaînes d'origine , et le complémentaire de dans . Supposons que . Ni ni ne sont alors vides. On applique l'hypothèse sur : il existe une arête , avec dans et . Il existe une chaîne d'origine et extrémité , alors, l'existence de , d'origine et extrémité montre que , une contradiction. On a donc montré que , il y a une chaîne d'origine et extrémité . On en déduit que est connexe.
Réciproquement, supposons que pour toute partition de en 2 parties (non vides) et , il existe une arête dont une extrémité est dans et l'autre dans . Considérons deux sommets et de . Notons l'ensemble des extrémités des chaînes d'origine , et le complémentaire de dans . Supposons que . Ni ni ne sont alors vides. On applique l'hypothèse sur : il existe une arête , avec dans et . Il existe une chaîne d'origine et extrémité , alors, l'existence de , d'origine et extrémité montre que , une contradiction. On a donc montré que , il y a une chaîne d'origine et extrémité . On en déduit que est connexe.
III-2 Cycles
Graphes
→
III Chaînes et cycles
→ III-2 Cycles
Proposition
De tout cycle, on peut extraire un cycle élémentaire.
Démonstration
Si
est un
-cycle, l'ensemble des couples d'entiers
tels que
et
n'est pas vide,
puisqu'il contient
. Il existe donc un tel couple
avec
minimal. On voit que
est un cycle élémentaire.
Proposition
De toute chaîne fermée de longueur impaire, on peut extraire un cycle de longueur impaire.
Démonstration
Par récurrence sur la longueur
de la chaîne fermée. Si
, la 1-chaîne fermée
est un 1-cycle. Supposons la propriété vraie pour toute
-chaîne fermée, avec
impair.
Si la
-chaîne fermée
est simple, c'est un cycle. Sinon, il existe
, avec
tel que
. On en déduit que les ensembles
et
sont égaux. Il y a deux possibilités:
-
et
. Posons alors
et
Ce sont deux chaînes fermées extraites de . La première a pour longueur
et la seconde
. On
a
impair, donc l'un des deux est impair, strictement plus petit que
. On peut appliquer l'hypothèse de récurrence à
ou
pour
obtenir un cycle impair extrait de
. La première a pour longueur
et la seconde
. On
a
impair, donc l'un des deux est impair, strictement plus petit que
. On peut appliquer l'hypothèse de récurrence à
ou
pour
obtenir un cycle impair extrait de
 .
.
-
et
. Posons alors
et
Ce sont deux chaînes fermées extraites de . La première a pour longueur
et la seconde
. On
a
impair, donc l'un des deux est impair, strictement plus petit que
. On peut appliquer l'hypothèse de récurrence à
ou
pour
obtenir un cycle impair extrait de
. La première a pour longueur
et la seconde
. On
a
impair, donc l'un des deux est impair, strictement plus petit que
. On peut appliquer l'hypothèse de récurrence à
ou
pour
obtenir un cycle impair extrait de
 .
.
Théorème
Si le degré minimum
d'un multigraphe
vaut au moins 2, alors il existe un cycle dans
.
Démonstration
Soit
une chaîne simple de longueur
maximale. Comme il y a au moins un sommet, et que son degré n'est pas nul, il y a au moins une arête, et
.
Si
est une boucle,
est un cycle. Sinon, comme
, il existe une arête
d'origine
et différente de
. Notons
le sommet tel que
.
La chaîne
a pour longueur
. Elle n'est donc pas simple. On en déduit qu'il existe
, avec
tel que
. Il existe donc
, avec
ou
tel que
et
. On a donc un cycle
.
Théorème
Si le degré minimum
d'un graphe simple
vaut au moins 2, alors il existe dans
un cycle élémentaire de longueur au moins égale à
.
Démonstration
Soit
une chaîne élémentaire de longueur
maximale. Comme il y a au moins un sommet, et que son degré n'est pas nul, il y a au moins une arête, et
.
Soit
un voisin de
. La chaîne
a pour longueur
, et n'est donc pas élémentaire. On en déduit que
est égal à l'un des
, pour un
, que nous appellerons l'indice du voisin
. Chacun des voisins de
a un indice différent. L'un d'eux au moins a donc un indice
. Puisque
est voisin de
,
est un cycle élémentaire, et sa longueur vaut au moins
.
Donnons enfin la caractérisation des graphes bipartis en termes de cycles:
Théorème
Un multigraphe
différent du 1-stable est biparti si et seulement si il n'existe pas dans
de cycle
de longueur impaire. En particulier, il ne doit pas avoir de boucle.
Remarquons que le nombre chromatique est inférieur ou égal ou égal à 2 si et seulement si est biparti ou 1-stable.
Démonstration
Si
est biparti, il existe une partition
telle que toute arête ait une extrémité dans
et une autre dans
. Si
est un
-cycle et si
, on voit, par récurrence sur
, que
pour
pair et
pour
impair. On sait que
. Donc
est pair.
Réciproquement, supposons que n'admette pas de cycle impair. Commençons par supposer que est connexe et . Choisissons un sommet . Notons
Comme
est connexe, il est clair que
. D'autre part, tout voisin d'un élément de
est dans
et tout voisin d'un élément de
est dans
. Comme
, on voit que ni
ni
ne sont vides. Il reste donc à prouver que
.
Si
il existe une chaîne paire
 et une chaîne impaire
et une chaîne impaire
 d'origine
et extrémité
. La concaténation
de ces deux chaînes est une chaîne fermée de longueur impaire. On peut donc en extraire un cycle impair, une contradiction.
Dans le cas où
n'est pas connexe, on voit que chacune des composantes connexes de
est bipartie ou
-stable et
lui-même est donc biparti ou 1-stable.
d'origine
et extrémité
. La concaténation
de ces deux chaînes est une chaîne fermée de longueur impaire. On peut donc en extraire un cycle impair, une contradiction.
Dans le cas où
n'est pas connexe, on voit que chacune des composantes connexes de
est bipartie ou
-stable et
lui-même est donc biparti ou 1-stable.
Réciproquement, supposons que n'admette pas de cycle impair. Commençons par supposer que est connexe et . Choisissons un sommet . Notons
 et une chaîne impaire
et une chaîne impaire
 d'origine
et extrémité
. La concaténation
de ces deux chaînes est une chaîne fermée de longueur impaire. On peut donc en extraire un cycle impair, une contradiction.
Dans le cas où
n'est pas connexe, on voit que chacune des composantes connexes de
est bipartie ou
-stable et
lui-même est donc biparti ou 1-stable.
d'origine
et extrémité
. La concaténation
de ces deux chaînes est une chaîne fermée de longueur impaire. On peut donc en extraire un cycle impair, une contradiction.
Dans le cas où
n'est pas connexe, on voit que chacune des composantes connexes de
est bipartie ou
-stable et
lui-même est donc biparti ou 1-stable.
III-3 Graphes eulériens
Graphes
→
III Chaînes et cycles
→ III-3 Graphes eulériens
Un cycle eulérien d'un multigraphe est un cycle qui visite toutes les arêtes et tous les sommets de . Un graphe eulérien est un multigraphe qui admet un cycle eulérien. Une chaîne eulérienne est une chaîne simple qui visite toutes les arêtes et tous les sommets de . Un graphe semi-eulérien est un multigraphe qui admet une chaîne eulérienne.
Notons que ces chaînes passent une fois et une seule par chaque arête, et au moins une fois par chaque sommet, mais qu'elles peuvent passer plusieurs fois par le même sommet. Des trois graphes suivants, le premier est eulérien, le second est semi-eulérien sans être eulérien, et le troisième n'est pas semi-eulérien.



Théorème
Soit
un multigraphe d'ordre au moins 2. Le multigraphe
est eulérien si et seulement si il est connexe et tous ses sommets sont de degré pair.
Démonstration
Remarquons d'abord qu'en ajoutant ou effaçant une boucle, on ne change pas la connexité, ni la parité du degré des sommets, ni l'existence d'un cycle eulérien. Nous pouvons donc supposer que
n'a pas de boucle.
Si
est eulérien, soit
une chaîne eulérienne. Elle visite tous les sommets, donc pour tout couple
de sommets, elle induit une chaîne d'extrémités
et
. Le graphe
est donc connexe. Soit
un sommet de
,
l'ensemble des arêtes incidentes à
et
. L'application
qui à une arête
incidente à
fait correspondre l'unique entier
tel que
et (
ou
) vérifie
Réciproquement, supposons que est connexe et que tous les sommets de sont de degré pair. Considérons une chaîne simple de longueur maximale . Nous allons montrer que est un cycle eulérien.
est un cycle eulérien.
Supposons d'abord que ne soit pas fermée, c'est-à-dire que
. Posons
et définissons
l'ensemble des arêtes incidentes à
visitées par
ne soit pas fermée, c'est-à-dire que
. Posons
et définissons
l'ensemble des arêtes incidentes à
visitées par
 ,
et
comme ci-dessus. On voit que
est un singleton et
vaut 2 pour
. On en déduit que
est impair. Comme
est de degré pair, il existe une arête
incidente à
qui n'est pas visitée par
,
et
comme ci-dessus. On voit que
est un singleton et
vaut 2 pour
. On en déduit que
est impair. Comme
est de degré pair, il existe une arête
incidente à
qui n'est pas visitée par
 et
est une
-chaîne simple, une contradiction. On a donc montré que
et
est une
-chaîne simple, une contradiction. On a donc montré que
 est un cycle.
est un cycle.
Supposons maintenant qu'il existe une arête non visitée par , et posons
. Comme
est connexe, il existe une chaîne
, et posons
. Comme
est connexe, il existe une chaîne  . Il est clair que
est visité par
. Il est clair que
est visité par
 . Il existe donc
tel que
. On voit que
. Il existe donc
tel que
. On voit que
Supposons enfin qu'il existe un sommet non visité par . Comme
est connexe, il existe une arête
incidente à
, et cette arête n'est pas visitée par
. Comme
est connexe, il existe une arête
incidente à
, et cette arête n'est pas visitée par
 , ce qui est impossible comme on vient de le voir.
, ce qui est impossible comme on vient de le voir.
On déduit alors du principe des bergers que est pair.
Réciproquement, supposons que est connexe et que tous les sommets de sont de degré pair. Considérons une chaîne simple de longueur maximale . Nous allons montrer que
 est un cycle eulérien.
est un cycle eulérien.
Supposons d'abord que
 ne soit pas fermée, c'est-à-dire que
. Posons
et définissons
l'ensemble des arêtes incidentes à
visitées par
ne soit pas fermée, c'est-à-dire que
. Posons
et définissons
l'ensemble des arêtes incidentes à
visitées par
 ,
et
comme ci-dessus. On voit que
est un singleton et
vaut 2 pour
. On en déduit que
est impair. Comme
est de degré pair, il existe une arête
incidente à
qui n'est pas visitée par
,
et
comme ci-dessus. On voit que
est un singleton et
vaut 2 pour
. On en déduit que
est impair. Comme
est de degré pair, il existe une arête
incidente à
qui n'est pas visitée par
 et
est une
-chaîne simple, une contradiction. On a donc montré que
et
est une
-chaîne simple, une contradiction. On a donc montré que
 est un cycle.
est un cycle.
Supposons maintenant qu'il existe une arête non visitée par
 , et posons
. Comme
est connexe, il existe une chaîne
, et posons
. Comme
est connexe, il existe une chaîne d'origine et extrémité . Posons et . Notons le plus petit élément de tel que ne soit pas visité par
 . Il est clair que
est visité par
. Il est clair que
est visité par
 . Il existe donc
tel que
. On voit que
. Il existe donc
tel que
. On voit que
est une -chaîne simple, une contradiction.
Supposons enfin qu'il existe un sommet non visité par
 . Comme
est connexe, il existe une arête
incidente à
, et cette arête n'est pas visitée par
. Comme
est connexe, il existe une arête
incidente à
, et cette arête n'est pas visitée par
 , ce qui est impossible comme on vient de le voir.
, ce qui est impossible comme on vient de le voir.
Corollaire
Soit
un multigraphe d'ordre au moins 2. Le multigraphe
est semi-eulérien si et seulement si
il est connexe et le nombre de ses sommets de degré impair est
ou
.
Démonstration
Si
 est une chaîne eulérienne de
dont les extrémités sont
et
, considérons le graphe
obtenu en ajoutant à
une arête
d'extrémités
et
. La chaîne
est un cycle eulérien de
. On en déduit que les degrés de tous les sommets de
(autres que
et
si
) sont pairs. La connexité de
est évidente exactement comme dans la démonstration du théorème.
est une chaîne eulérienne de
dont les extrémités sont
et
, considérons le graphe
obtenu en ajoutant à
une arête
d'extrémités
et
. La chaîne
est un cycle eulérien de
. On en déduit que les degrés de tous les sommets de
(autres que
et
si
) sont pairs. La connexité de
est évidente exactement comme dans la démonstration du théorème.
Réciproquement, si a deux sommets distincts de degré impair, et , le graphe défini comme ci-dessus a tous ses sommets de degré pair. Si est connexe, l'est aussi et on peut appliquer le théorème à . Si est un cycle eulérien de
, il visite forcément
et, en retirant
de
est un cycle eulérien de
, il visite forcément
et, en retirant
de
 , on obtient une chaîne eulérienne de
.
, on obtient une chaîne eulérienne de
.
 est une chaîne eulérienne de
dont les extrémités sont
et
, considérons le graphe
obtenu en ajoutant à
une arête
d'extrémités
et
. La chaîne
est un cycle eulérien de
. On en déduit que les degrés de tous les sommets de
(autres que
et
si
) sont pairs. La connexité de
est évidente exactement comme dans la démonstration du théorème.
est une chaîne eulérienne de
dont les extrémités sont
et
, considérons le graphe
obtenu en ajoutant à
une arête
d'extrémités
et
. La chaîne
est un cycle eulérien de
. On en déduit que les degrés de tous les sommets de
(autres que
et
si
) sont pairs. La connexité de
est évidente exactement comme dans la démonstration du théorème.
Réciproquement, si a deux sommets distincts de degré impair, et , le graphe défini comme ci-dessus a tous ses sommets de degré pair. Si est connexe, l'est aussi et on peut appliquer le théorème à . Si
 est un cycle eulérien de
, il visite forcément
et, en retirant
de
est un cycle eulérien de
, il visite forcément
et, en retirant
de
 , on obtient une chaîne eulérienne de
.
, on obtient une chaîne eulérienne de
.
III-4 Graphes hamiltoniens
Graphes
→
III Chaînes et cycles
→ III-4 Graphes hamiltoniens
Proposition
Les graphes simples
et
sont hamiltoniens si et seulement si
.
En effet, dans un graphe simple, la longueur d'un cycle est au moins 3.
Théorème
Si
est un graphe simple d'ordre
tel que
pour toute paire
de sommets non voisins, on a
, alors
est hamiltonien.
Démonstration
Considérons dans
une chaîne élémentaire de longueur maximale
. On voit facilement que
et que les voisins de
et ceux de
sont tous visités par
 . Deux cas se présentent:
. Deux cas se présentent:
 est un cycle élémentaire de longueur
, que nous réécrivons
, avec
. Nous allons montrer que
est un cycle élémentaire de longueur
, que nous réécrivons
, avec
. Nous allons montrer que
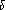 est un cycle hamiltonien.
est un cycle hamiltonien.
Soit un sommet qui n'est pas visité par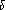 . S'il est voisin d'un des
, alors
est une chaîne élémentaire de longueur
, une contradiction. On en déduit que les voisins de
ne rencontrent pas les
sommets visités par
. S'il est voisin d'un des
, alors
est une chaîne élémentaire de longueur
, une contradiction. On en déduit que les voisins de
ne rencontrent pas les
sommets visités par
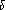 , donc
. De même, les voisins de
sont parmi les
sommets visités par
, donc
. De même, les voisins de
sont parmi les
sommets visités par
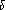 autres que
, et
. On a donc
, ce qui mène à une contradiction avec le fait que
et
ne sont pas voisins.
autres que
, et
. On a donc
, ce qui mène à une contradiction avec le fait que
et
ne sont pas voisins.
 . Deux cas se présentent:
. Deux cas se présentent:
- Si
et
sont voisins, posons
- Si
et
ne sont pas voisins,
posons
et
On a et . D'après l'hypothèse sur , on a , donc et ont un élément commun , avec . Posons alors
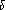 est un cycle élémentaire de longueur
, que nous réécrivons
, avec
. Nous allons montrer que
est un cycle élémentaire de longueur
, que nous réécrivons
, avec
. Nous allons montrer que
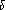 est un cycle hamiltonien.
est un cycle hamiltonien.
Soit un sommet qui n'est pas visité par
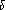 . S'il est voisin d'un des
, alors
est une chaîne élémentaire de longueur
, une contradiction. On en déduit que les voisins de
ne rencontrent pas les
sommets visités par
. S'il est voisin d'un des
, alors
est une chaîne élémentaire de longueur
, une contradiction. On en déduit que les voisins de
ne rencontrent pas les
sommets visités par
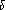 , donc
. De même, les voisins de
sont parmi les
sommets visités par
, donc
. De même, les voisins de
sont parmi les
sommets visités par
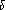 autres que
, et
. On a donc
, ce qui mène à une contradiction avec le fait que
et
ne sont pas voisins.
autres que
, et
. On a donc
, ce qui mène à une contradiction avec le fait que
et
ne sont pas voisins.
Corollaire
Si
est un graphe simple d'ordre
tel que
, alors
est hamiltonien.
IV Arbres
Graphes
→ IV Arbres
Une forêt est un multigraphe sans cycle. En particulier, c'est un graphe simple. Un arbre est un graphe connexe sans cycle. Voici quelques arbres.



IV-2 Caractérisation des arbres
IV-1 Préliminaires
Un sommet pendant d'un graphe est un sommet de degré 1. Si est un sommet pendant, il existe une arête incidente à et une seule.Proposition
Démonstration
On rappelle que
est un graphe simple.
Soit
une chaîne élémentaire de longueur maximale. Comme n'est pas vide, il y a au moins une arête, donc . Le seul voisin de est . En effet, si est un autre voisin de , soit est l'un des , avec et est un cycle, une contradiction, soit non, auquel cas est une une chaîne élémentaire de longueur , encore une contradiction. On en déduit , et de même .
Corollaire
Démonstration
Par récurrence sur
. Pour
, il n'y a pas de boucle, donc
et
. Si
, il y a au moins deux sommets. Comme
est connexe, il y a au moins une chaîne qui les joint, donc
n'est pas vide. Il y a donc aumoins un sommet pendant
. Soit
l'unique arête adjacente à
. Le graphe
est un arbre d'ordre
. On peut lui appliquer l'hypothèse de récurrence. On a donc
donc .
Proposition
Soit
et
deux chaînes simples distinctes d'origine et extrémité dans un multigraphe . De la chaîne fermée , on peut extraire un cycle.
Démonstration
Par récurrence sur
. Si
, il n'est pas possible que
, il n'y a donc rien à démontrer.
Supposons la propriété vraie si la somme des longueurs est strictement plus petite que
. Si
est simple, c'est un cycle. Sinon, il existe une arête visitée deux fois par
. Comme
 et
et
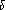 sont simples, une des visites est dans
sont simples, une des visites est dans
 et l'autre dans
: il existe
et
tels que
=
. Il y a deux possibilités:
et l'autre dans
: il existe
et
tels que
=
. Il y a deux possibilités:
 et
et
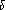 sont simples, une des visites est dans
sont simples, une des visites est dans
 et l'autre dans
: il existe
et
tels que
=
. Il y a deux possibilités:
et l'autre dans
: il existe
et
tels que
=
. Il y a deux possibilités:
- et . On a alors soit soit . Dans les deux cas on peut appliquer l'hypothèse de récurrence pour obtenir un cycle extrait de .
- et . On a alors soit soit . Dans les deux cas on peut appliquer l'hypothèse de récurrence pour obtenir un cycle extrait de .
Corollaire
Dans un multigraphe
, il existe un cycle si et seulement si il existe deux chaînes simples distinctes qui ont même origine et même extrémité.
Enfin, dans un graphe connexe , un isthme est une arête telle que le graphe ne soit pas connexe.
Proposition
Dans un graphe connexe, une arête est un isthme si et seulement si elle n'est visitée par aucun cycle.
Démonstration
Supposons d'abord que
est visité par un cycle. On peut écrire
), avec
. Soit
et
deux sommets de
. Comme
est connexe, il existe une chaîne simple 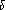 ne visite pas
, on pose
. Dans le cas contraire, il existe un unique
tel que
. On ``remplace
dans
ne visite pas
, on pose
. Dans le cas contraire, il existe un unique
tel que
. On ``remplace
dans
 par le grand arc de
par le grand arc de
 '', c'est-à-dire qu'on pose
'', c'est-à-dire qu'on pose
 de
d'origine
et extrémité
. La chaîne
est fermée et simple: c'est un cycle qui visite
.
de
d'origine
et extrémité
. La chaîne
est fermée et simple: c'est un cycle qui visite
.
Si
 ne visite pas
, on pose
. Dans le cas contraire, il existe un unique
tel que
. On ``remplace
dans
ne visite pas
, on pose
. Dans le cas contraire, il existe un unique
tel que
. On ``remplace
dans
 par le grand arc de
par le grand arc de
 '', c'est-à-dire qu'on pose
'', c'est-à-dire qu'on pose
si et , et
si et . Il existe dans tous les cas une chaîne de , d'origine et extrémité . On en déduit que est connexe et n'est pas un isthme. Réciproquement, si n'est pas un isthme, notons et les extrémités de . Comme est connexe, il existe une chaîne simple
 de
d'origine
et extrémité
. La chaîne
est fermée et simple: c'est un cycle qui visite
.
de
d'origine
et extrémité
. La chaîne
est fermée et simple: c'est un cycle qui visite
.
Corollaire
Soit
et
deux arbres, composantes connexes distinctes d'une forêt
. Soit
et
. Posons
.
Le graphe simple
est encore une forêt.
En effet, est un isthme du graphe connexe . Un cycle de doit visiter donc rester dans , une contradiction.
IV-2 Caractérisation des arbres
On rappelle sans démonstration un théorème classique:
Théorème
Soit
un
-espace vectoriel de dimension
, et
une famille finie d'éléments de
. Les propriétés suivantes sont équivalentes:
Le théorème suivant est tout-à-fait analogue au théorème précédent:
- est une base de .
- Pour tout vecteur , il existe une famille de scalaires telle que et une seule.
- est une famille génératrice de et pour tout la famille obtenue en enlevant à ne l'est pas ( est génératrice minimale).
- est libre et quelle que soit la valeur de , la famille ne l'est pas ( est libre maximale).
- est une famille génératrice de et .
- est une famille libre et .
Théorème
Soit
un multigraphe. On note
son ordre et
le nombre de ses arêtes. Les propriétés suivantes sont équivalentes:
- est un arbre.
- Pour tout couple de sommets, il existe une chaîne simple d'origine et extrémité et une seule.
- est connexe, et toute arête de est un isthme ( est connexe minimal).
- est une forêt, et pour toute arête , admet un cycle ( est une forêt maximale).
- est connexe et .
- est une forêt, et .
Démonstration
- [ ] La connexité est équivalente à l'existence de chaînes simples de à pour tous sommets et . D'autre part, grâce au lemme allerretour , on voit que l'existence d'un cycle équivaut à celle de deux chaînes simples ayant même origine et même extrémité.
- [ ] D'après la proposition isthme , dans un graphe connexe, l'existence d'un isthme est équivalente à la non-existence d'un cycle.
- [ ] D'après le corollaire ajout , si une forêt n'est pas connexe, on peut lui ajouter une arête sans créer de cycle. Réciproquement, si est un arbre et , alors il existe une chaîne simple d'origine et extrémité dans , en est une autre dans , ce qui, grâce à la proposition allerretour montre que n'est pas une forêt.
- [ ] C'est une conséquence du corollaire nombre .
- [ ] Parmi les sous-graphes couvrants de qui sont connexes, il y en a au moins un qui est minimal. C'est un arbre. D'après , on a . Or . On en déduit .
- [ ] Une forêt est un graphe simple. On en déduit que parmi les forêts sur dont est un graphe couvrant, il en existe une qui est maximale. C'est un arbre. D'après , on a . Or . On en déduit .
IV-3 Arbres couvrants
Un arbre couvrant d'un multigraphe est un sous-graphe couvrant de qui est un arbre. Si un graphe a un arbre couvrant, il est connexe. Le théorème précédent montre que la réciproque est vraie. Nous présentons deux algorithmes naturels pour trouver un arbre couvrant d'un multigraphe connexe.
Données: Un multigraphe connexe G = (S,A) Sortie: Une partie A' de A telle que G'=(S, A') est un arbre.
A' <- {} tant que $G'$ n'est pas connexe choisir une composante connexes C de G' choisir une arête e de A liant C et S \ C faire A' <- A' union {e} fin tant que
L'existence de l'arête est due au fait que est connexe. L'adjonction de à ne change pas le fait que est une forêt. L'algorithme s'arrête donc bien quand est un arbre.
Cet algorithme a une variante adaptée aux graphes valués: on définit le poids d'un sous-graphe comme la somme des coûts de toutes les arêtes de ce sous-graphe, et on cherche un arbre couvrant de poids minimal.
Données: Un multigraphe valué connexe G = (S,A,c) Sortie: Une partie A' de A telle que G'=(S, A') est un arbre et le poids total de A' est minimal.
numéroter les éléments de A par poids croissant: c(e_1) <= ... <= c(e_m) A' <- {} pour i allant de 1 à m faire si (e_i n'est pas une boucle et si) les extrémités de e_i sont sur des composantes connexes différentes de G' faire A' <- A' union {e_i} fin si fin tant que
Cet algorithme, qui prend en priorité les arêtes de poids faible, est appelé glouton pour la même raison qui fait qu'en informatique les arbres sont représentés avec leurs racines en haut et les feuilles en bas.
Il existe une méthode duale pour extraire un arbre couvrant, qui consiste à couper les cycles tant qu'il y en a. Nous allons l'énoncer pour un multigraphe quelconque.
Données: Un multigraphe G = (S,A) à e composantes connexes. Sortie: A' est une partie de A telle que G'=(S,A') est une forêt à e composantes connexes.
A' <- A tant qu'il existe un cycle dans G' choisir un cycle C dans G' choisir une arête e visitée par C faire A' <- A' \ {e} fin tant que
Comme on l'a vu plus haut, le fait d'enlever une arête visitée par un cycle ne change rien à la connexité. Le nombre de composantes connexes de est donc le même que celui de . En particulier, si est connexe, est un arbre couvrant de . En général, combien de fois la boucle interne de l'algorithme s'exécute-t'elle ? Appelons ce nombre. On voit que est le nombre d'arêtes qu'on a enlevées. La proposition suivante montre que ne dépend pas des choix faits dans l'algorithme, mais seulement du multigraphe . Nous appellerons le nombre de cycles indépendants de .
Proposition
Dans l'algorithme précédent, la boucle interne s'exécute
fois, avec
où est l'ordre de , son nombre d'arêtes, et son nombre de composantes connexes.
Démonstration
Notons
les
composantes connexes d'une forêt
à
sommets et
arêtes. Chaque
est un arbre, on a donc
.
Comme
est réunion disjointe des
et
réunion disjointe des
, on a
Si maintenant est un multigraphe quelconque et qu'on exécute l'algorithme, le résultat est une forêt qui a le même nombre de sommets et le même nombre de composantes connexes que . Son nombre d'arêtes est . Or on vient de montrer que , d'où le résultat.
Si maintenant est un multigraphe quelconque et qu'on exécute l'algorithme, le résultat est une forêt qui a le même nombre de sommets et le même nombre de composantes connexes que . Son nombre d'arêtes est . Or on vient de montrer que , d'où le résultat.
IV-4 Théorème de Cayley
On s'intéresse ici aux arbres couvrants de la clique , ou plutôt à leur nombre. On voit facilement que et sont des arbres et que a trois arbres couvrants.



Il est plus difficile d'établir que les arbres couvrants de sont au nombre de 16, mais il n'y en a que deux à isomorphisme près. Supposons désormais . Nous allons décrire une opération de codage qui à tout arbre dont l'ensemble des sommets est fait correspondre une famille de éléments de de la façon suivante.
Données: Un arbre T = (S, A) d'ensemble de sommets S = [1,n] Sortie: le tableau b contient n-2 entiers de [1,n]
pour i de 1 à n-2 faire s <- le plus petit sommet pendant de T e <- l'arête incidente à s b[i] <- le voisin de s dans T S <- S \ {s} A <- A \ {e} fin pour
Voici la suite des opérations qui donne l'encodage d'un certain arbre couvrant de .








Le résultat final est donc la famille . L'opération de décodage se décrit de la même façon:
Données: Un tableau b de n-2 entiers de [1,n] Sortie: T = ([1,n], A) est un arbre
A <- {} S <- [1,n]
pour i de 1 à n-2 faire s <- le plus petit élément de S qui n'est égal à aucun b[j] avec i <= j <= n-2. A <- A union {{s,b[i]}} S <- S \ {s} fin pour
A <- A union {S}
Comme a éléments et ne prend que valeurs, on peut toujours trouver . Pour prouver que le graphe obtenu est un arbre, il suffit de remarquer qu'à tout moment contient un sommet et un seul dans chaque composante connexe de . Comme n'a pas pu être enlevé de aux tours précédents, il est encore dans et l'arête réunit deux composantes connexes différentes: il ne peut se créer de cycle. Après la fin de la boucle, S ne contient que deux éléments, appartenant aux deux composantes connexes de . Enfin, est une forêt à arêtes, c'est donc bien un arbre. Voici la suite d'opérations décrivant le décodage de :









On voit que les opérations de codage et de décodage sont inverses l'une de l'autre. On a donc une bijection entre l'ensemble des arbres couvrants de et . On a donc prouvé le
Théorème [de Cayley]
Pour tout
, une
-clique a exactement
arbres couvrants.