Inégalités, inéquations
Objectifs
Majorer, minorer, encadrer, voici les techniques de base de l'analyse et ce cours a pour but de vous présenter ces techniques et de vous y entraîner. Il fournira une approche de la notion de limite. Il s'agit d'un cours d'approfondissement, notamment en ce qui concerne la difficulté des exercices. Il s'adresse à des étudiants post-bac, ayant une certaine pratique des inégalités.
Pour une approche basique des notions d'inégalités, intervalles et encadrements, on consultera avec le plus grand profit du cours DOC Inégalités, intervalles, inéquations .
Sommaire
A. Inégalités. Encadrements. Inéquations
- Encadrements
- Bornes d'une partie, d'une expression
- Borner une fraction
- Techniques d'encadrement
- Exercices de déduction d'inégalités simples
- Autres exercices classiques
- Inéquations : Exercices
- Inéquations avec paramètres
B. Implication entre inégalités
C. Applications aux limites.
- Limite finie d'une suite
- Limite infinie d'une suite
- Théorème de comparaison pour les suites
- Une définition de limite
- Méthode
- Un exemple simple
- Approche de la définition de la limite
- Interprétation
Encadrements
Voici quelques exercices pour tester vos connaissances et votre pratique des inégalités. Si vous rencontrez des difficultés ou que vous manquiez d'assurance, n'hésitez pas à consulter les parties [A], [B] et [C] du cours Activité inconnue .
- Encadrement d'une différence
- Encadrement de |x|
- Encadrement d'un carré
- Encadrement d'un produit
- Encadrement 1
- Encadrement 2
- Zone d'inégalité
On rappelle les résultats suivants que l'on cherchera à démontrer pour une meilleure appropriation.
- Si , alors l'inégalité est équivalente à : { ET }, c'est à dire :
- Si , alors l'inégalité est équivalente à : { OU },
Pour le calcul propositionnel, les ET et OU, consultez cette page .
Bornes d'une partie, d'une expression
Avant d'étudier cette page, on consultera, si nécessaire, la page encadrement du cours Activité inconnue .
 .
Soit
une partie non vide de
.
.
Soit
une partie non vide de
.
- On dit que est majorée dans s'il existe un réel , appelé majorant de , tel que tous les éléments de sont inférieurs ou égaux à .
- On dit que est minorée dans s'il existe un réel , appelé minorant de tel que tous les éléments de sont supérieurs ou égaux à .
- On dit que est bornée dans s'il existe deux réels et tels que tous les éléments de sont supérieurs à et inférieurs à .
Tous les réels de : [[ sont des majorants de . Ceux de : ] - ] en sont des minorants.
On notera que appartient à , mais que -1 n'y appartient pas.
il est facile de voir que est minoré par 0, et majoré par 2 puisque et sont supérieurs ou égaux à 1
Le maximum 2 est atteint pour , c'est donc le meilleur possible (et il appartient à ).
Si on fait tendre et vers , on voit que tend vers 0, d'aussi près que l'on veut. 0 est donc le meilleur minimum (mais il n'appartient pas à ).
Majoration sous condition
-
SolutionPar hypothèse le réel est dans l'intervalle , l'expression de la valeur absolue d'un produit et l'inégalité triangulaire nous permettent de majorer le numérateur :
D'autre part le dénominateur vaut dans l'intervalle considéré donc est minoré par 2. En combinant ces deux résultats, on obtient l'implication cherchée.
SolutionQuand est positif, exp est positif et majoré par 1, on obtient donc :
Quand est supérieur à 3, alors on a , donc on obtient
d'où l'inégalité : qui permet d'obtenir l'implication
SolutionPar hypothèse, si , est compris entre et et comme la fonction cosinus est paire et décroissante sur , l'expression est positif et minoré par . De plus est minoré par et est majoré par 5. On obtient donc
Pour , on a : (on est aussi autorisé à prendre une calculatrice...). Ce qui est équivalent à d'où on tire :.
Limite finie d'une suite
La définition suivante est formellement la même dans ou , avec cette différence : la notation désigne une valeur absolue dans et un module dans .
Soit une suite numérique, à valeur dans ou . On dit que la suite converge vers le nombre si :
tel que
On note alors :Graphiquement, cela signifie qu'une valeur étant fixée, alors au-delà du rang (qui dépend du choix de ), tous les termes de rang supérieurs à sont dans l’intervalle [ ] dans le cas réel, et dans le disque de centre et de rayon dans le cas complexe.
Dans le graphique ci-dessous, pour une suite convergeant vers 2, on a tracé les points de coordonnée pour . On constate que rapidement tous les points se situent à l'intérieur de la bande entre et .
À partir de quel entier la quantité sera-t-elle inférieure à ?
Ici, on résout des inéquations : On se donne donc un petit dans et on cherche les vérifiant : on a les équivalences suivantes
La valeur qui répond à la définition de la limite est la valeur trouvée, mais, comme elle n'est très probablement pas entière, on prendra où est la partie entière de .
Pour , on trouve .
On notera que l'on a ici raisonné par équivalence.
= = .
On peut minorer par , puis par 10, ce qui est acquis dès que .On obtient ainsi
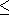
Pour , on trouve , compatible avec l'hypothèse . Ce résultat est moins précis que le résultat précédent mais on a raisonné directement par majoration et minoration ce qui est dans l'esprit de ce document.
Limite infinie d'une suite
Soit une suite à valeur dans .
- On dit que
tend vers
lorsque
tend vers
si
tel que
On note alors : - On dit que
tend vers
lorsque
tend vers
si
tel que
On note alors :
Un certain nombre de suites "de référence" tendent vers . Par exemple, les suites (avec ); ; ; ... Ces suites seront largement utilisées pour des majorations ou minorations de suites plus complexes, en utilisant les théorèmes de comparaison, voir par exemple un Théorème de comparaison pour les suites .
Même question avec les suites géométriques de raison .
On peut démontrer par récurrence les formules et .
Pour traiter la suite géométrique, poser avec . Commencer à développer à l'aide de la formule du binôme de Newton et minorer judicieusement.
Théorème de comparaison pour les suites
Cet énoncé résulte facilement de la définition d'une suite tendant vers l'infini.
Soit et deux suites vérifiant :
- Il existe un rang tel que pour tout
- La suite tend vers .
Solution : Cette suite est positive. On minore le numérateur et on majore le dénominateur et on obtient et . On en déduit une minoration de par le terme général d'une suite qui tend vers l'infini : . Cela démontre l'égalité
Pour rester dans l'esprit du document, on procéde par minoration:
On se donne un nombre réel et on cherche un entier répondant à la définition.
Si on choisit tel que , on peut écrire les inégalités : , et en particulier .
il suffit donc de choisit pour le plus petit entier naturel tel que , par exemple , où est la partie entière du réel .
Ici, nous avons montré que la suite minorante tend vers l'infini et nous avons ainsi conclu avec la définition sans invoquer le théorème.
Les facteurs correspondants à des valeurs de comprises entre et sont supérieurs ou égaux à . Les autres sont supérieurs à 1, on obtient donc . La suite est une suite géométrique de raison supérieure à 1, donc elle tend vers , ainsi que , grâce au théorème de comparaison.
Une définition de limite
Soit
un sous-ensemble de
et
une fonction définie sur
à valeurs dans
.
Soit
un réel (n'appartenant pas nécessairement à
, mais tel que
soit « définie au voisinage de
»), et
un réel.
On dit que
admet
pour limite au point
, lorsque :
Pour tout réel
, il existe un réel
, tel que, pour tout
dans
avec
,
on ait
Cette proposition s'écrit aussi.
et
On note , ou .
Commentaires sur cette définition
- Cette définition de la limite fait appel, on le voit, à des inégalités, ce qui justifie sa présence dans ce document qui, pour autant, n'est pas consacré aux questions de limite.
- On notera que la valeur de la limite est ici supposée connue.
- Calcul d'un\(epsilon\)
- Aide visuelle. Le nombre étant donné, trouver en étant aidé visuellement.
En attendant d'avoir des théorèmes sur les limites, on voit que pour démontrer qu'une fonction admet la limite quand tend vers , on est amené, pour un donné, à trouver un nombre (qui n'est pas unique, bien sûr) vérifiant certaines propriétés. La méthode est décrite à cette page .
Méthode
Une lecture approximative de la définition de la limite peut conduire à une direction de travail peu précise. Certains la réduisent au schéma suivant : si tend vers , alors tend vers , mettant la priorité au comportement de , qui va entraîner celui de . La démarche de la démonstration est exactement inverse.
Revenons à un peu de logique mathématique. Dans une implication , le but final est la proposition , c'est donc ce que l'on doit avoir en perspective dès le début.
- On cherche donc à majorer par , sous certaines conditions sur . Pour cela, il peut être très utile de chercher un majorant plus simple de faisant apparaitre la quantité . On vise à obtenir une inégalité du type , avec .
- Grace à cette inégalité, pour un
donné et pour obtenir l'inégalité cherchée, il suffit d'avoir
.
Une valeur de
en découle :
.
(On notera que cette valeur de dépend du que l'on s'est donné). Ce qui achève la preuve.
On a ainsi trouvé un intervalle sur l'axe des abscisses (et qui doit être dans l'ensemble de définition) dans lequel il suffit de prendre les valeurs de dans A, pour avoir , c'est à dire pour que que soit dans l'intervalle .
Montrer, en utilisant la définition ci-dessus, que la fonction définie sur par admet pour limite 0 lorsque tend vers .
Preuve : On note d'abord que le trinôme admet 1 et -5 pour racines. Donc , et on a fait apparaitre la quantitéComme tend vers , on peut supposer que est compris entre et , mais on introduit donc une condition sur (dont il faudra tenir compte) qui s'écrit (*).
Comme est compris entre et , . Cette condition nous permet donc de majorer par .
Donc est majoré par
Soit , pour que l'inégalité soit vérifiée, il suffit que la condition (*) soit vérifiée et qu'on ait , c'est-à-dire . Donc on choisit .
Application. Si on se donne par exemple, on obtient et on sait alors que toutes les valeurs de se trouvant dans l'intervalle ont des images par dans l'intervalle .
Un exemple simple
-
avec la condition
.
Solution
Si la condition est vérifiée, est majoré par et on peut écrire : -
avec la condition
Solution
Si est compris entre 1/2 et 3/2, (on est alors sûr que la fonction est définie), on minore par (faire un dessin sur la droite réelle en plaçant , , et 2, et on majore par . On peut donc écrire quesi x est compris entre 1/2 et 3/2 ,
-
avec la condition
Solution= =
La fonction est définie si et seulement si n'est pas nul, nous allons donc supposer que est entre et , alors est majoré par et est majoré par pour faire simple.
Solution
Au voisinage de 1, on peut supposer que , et donc que (*) condition qui sera réutilisée. De plus
On a donc obtenu :
Soit , pour que l'inégalité soit vérifiée, il suffit que la condition (*) soit vérifiée et qu'on ait , c'est-à-dire .
On choisit donc
Conclusion : . Ce qui prouve le résultat cherché.
Solution
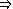
-
. On doit choisir
inférieur à 1 car la majoration n'est démontrée que pour
.
 )
)
-
.
-
.